2024-2025学年北师大版数学八（上）1.2一定是直角三角形吗同步训练
试卷更新日期：2024-07-10 类型：同步测试
一、选择题
-
1. 下列各组数中，能构成直角三角形的是（ ）A、4，5，6 B、1，1， C、6，8，11 D、5，12，232. 在单位长度为1的正方形网格中，下面的三角形是直角三角形的是（ ）A、
B、
C、
D、
3. 下列各组长度的线段，不能组成直角三角形的是（ ）A、5，12，13 B、 C、2，3，4 D、6，8，104. 古埃及人曾经用如图所示的方法画直角：用13个等距的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第1个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，这样做的道理是( )
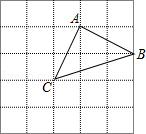
A、直角三角形两个锐角互余 B、三角形内角和等于180° C、三角形两边之和大于第三边，两边之差小于第三边 D、如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形5. 已知△ABC中，a、b、c分别是∠A，∠B，∠C的对边，下列条件不能判断△ABC是直角三角形的是 （ ）A、∠A＝∠C－∠B B、a2＝b2－c2 C、a：b：c＝2：3：4 D、a＝ ，b＝ ，c＝16. 如图，图中小正方形的边长都为1，△ABC的顶点都在格点上，则△ABC是（ ）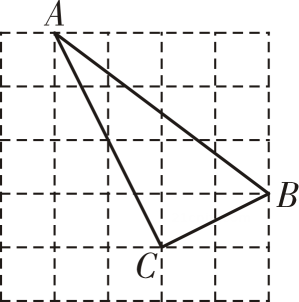
A、直角三角形 B、锐角三角形 C、钝角三角形 D、无法判断7. 下列条件中，不能判定△ABC是直角三角形的是（ ）A、∠A＝∠B+∠C B、a：b：c＝5：12：13 C、a2＝（b+c）（b-c） D、∠A：∠B：∠C＝3：4：58. 下列各组数中能作为直角三角形三边长度的是（ ）A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，8二、填空题
-
9. 在中，若 ， 则 ．10. 如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，连接AB、BC ， 则∠ABC的度数为 ．
11. 如图，在△ABC中，D是BC上一点，已知AB=15，AD=12，AC=13，CD=5，则BC的长为.
12. 下列条件：①∠C＝∠A－∠B；②∠A：∠B：∠C＝5∶2∶3；③a＝c，b＝c；④a∶b∶c＝1∶2： ， 则能确定△ABC是直角三角形的条件有个．13. 如图，在△ABC中，已知∠A为钝角，边AB，AC的中垂线分别交BC于点D，E．若BD2+CE2=DE2 ， 则∠A= ．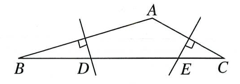
三、解答题
-
14. 如图，在四边形中， ， BD平分 ， ， E为上一点， ， ， 求证： ．
15. 如图，在一条笔直的东西方向的公路上有A、B两地，相距500米，且离公路不远处有一块山地C需要开发，已知C与A地的距离为300米，与B地的距离为400米，在施工过程中需要实施爆破，为了安全起见，爆破点C周围半径260米范围内不得进入．
(1)、山地C距离公路的垂直距离为多少米？(2)、在进行爆破时， A、B两地之间的公路是否有危险需要暂时封锁？若需要封锁，请求出需要封锁的公路长．四、作图题
-
16. 如图，正方形网格中的每个小正方形的边长都是1，每个小方格的顶点叫做格点，以格点为顶点分别按下列要求画三角形(涂上阴影)．
(1)、在图1中画一个直角三角形，使它的三边长都是有理数．(2)、在图2、图3中分别画两个不全等的直角三角形，使它的三边长都是无理数．17. 如图是一个6×6的正方形网格，每个小正方形的顶点都是格点，Rt△ABC的顶点都是图中的格点，其中点A、点B的位置如图所示，你能找到几个这样的C点？把它们都画出来。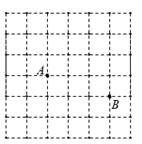
五、综合题
