北师大版数学八(上)1.1探索勾股定理 同步测试
试卷更新日期:2024-07-10 类型:同步测试
一、选择题
-
1. 在 Rt△ABC 中, ∠C = 90° , AB = 3 , AC = 2, 则 BC 的值( )A、 B、 C、 D、2. 《九章算术》是我国古代最重要的数学著作之一,它的出现标志着中国古代数学形成了完整的体系.“折竹抵地”问题源自《九章算术》﹔“今有竹高一丈,末折抵地,去本四尺,问折者高几何?”翻译成数学问题是:如图所示, 中, , 尺, 尺,求AC的长.则AC的长为( )
 A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺3. 如图,网格中每个小正方形的边长均为1,点A , B , C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D , 则CD的长为( )
A、4.2尺 B、4.3尺 C、4.4尺 D、4.5尺3. 如图,网格中每个小正方形的边长均为1,点A , B , C都在格点上,以A为圆心,AB为半径画弧,交最上方的网格线于点D , 则CD的长为( ) A、 B、 C、2.2 D、34. 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( )
A、 B、 C、2.2 D、34. 图1是边长为1的六个小正方形组成的图形,它可以围成图2的正方体,则图1中正方形顶点A、B在围成的正方体中的距离是( ) A、0 B、1 C、 D、5. 满足下列条件的△ABC不是直角三角形的是( )A、AC=1,BC= ,AB=2 B、AC:BC:AB=3:4:5 C、∠A:∠B:∠C=1:2:3 D、∠A:∠B:∠C=3:4:56. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、137. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A、0 B、1 C、 D、5. 满足下列条件的△ABC不是直角三角形的是( )A、AC=1,BC= ,AB=2 B、AC:BC:AB=3:4:5 C、∠A:∠B:∠C=1:2:3 D、∠A:∠B:∠C=3:4:56. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、137. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )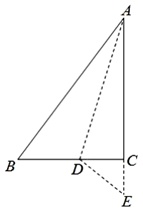 A、1cm B、cm C、cm D、2cm8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时, 梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5m,则小巷的宽为( ).
A、1cm B、cm C、cm D、2cm8. 如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时, 梯子底端到左墙角的距离BC为0.7m,梯子顶端到地面的距离AC为2.4m.如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A'D为1.5m,则小巷的宽为( ).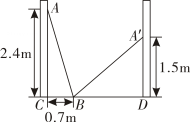 A、2.4m B、2m C、2.5m D、2.7m
A、2.4m B、2m C、2.5m D、2.7m二、填空题
-
9. 直角三角形两直角边长分别为5和12,则它斜边上的高为 .
10. 如图是一个三级台阶,它的每一级的长、宽、高分别为 , 和 , 和 是这个台阶的两个端点, 点上有一只蚂蚁想到 点去吃可口的食物,则它所走的最短路线长度为 . 11. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
11. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .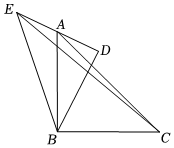 12. 在平面直角坐标系中,将一副三角板按如图所示的方式摆放,BO、DO分别与.动点在边上运动,动点在边上运动,的中点的坐标为 , 则的最小值是.
12. 在平面直角坐标系中,将一副三角板按如图所示的方式摆放,BO、DO分别与.动点在边上运动,动点在边上运动,的中点的坐标为 , 则的最小值是. 13. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
13. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
三、作图题
-
14. 用刻度尺和圆规作一条线段 ,使它的长度为cm.(保留作图痕迹)15. 如图,在长方形纸片ABCD中,AB=CD=5,AD=BC=3.
 (1)、尺规作图:在边BC找一点P,使得△ABP沿直线AP折叠时,B点恰好落在边CD上:(写出作法过程,保留作图痕迹,不需证明)(2)、求BP的长.
(1)、尺规作图:在边BC找一点P,使得△ABP沿直线AP折叠时,B点恰好落在边CD上:(写出作法过程,保留作图痕迹,不需证明)(2)、求BP的长.四、解答题
-
16. 如图,折叠矩形的一边 ,使点 落在 边的点 处,已知AB=8cm,BC=10cm,求 的长
 17. 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10点E是CD的中点,求AE的长.
17. 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10点E是CD的中点,求AE的长.
五、实践探究题
-
18. 定义:在任意中,如果一个内角度数的2倍与另一个内角度数的和为 , 那么称此三角形为“倍角互余三角形”.
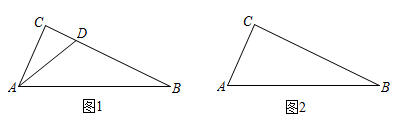 (1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.
(1)、【基础巩固】若是“倍角互余三角形”, , , 则;(2)、【尝试应用】如图1,在中, , 点为线段上一点,若与互余.求证:是“倍角互余三角形”;(3)、【拓展提高】如图2,在中, , , , 试问在边上是否存在点 , 使得是“倍角互余三角形”?若存在,请求出的长;若不存在,请说明理由.六、综合题
-
19. 在长方形纸片ABCD中,点E是边CD上的一点,将△AED沿AE所在的直线折叠,使点D落在点F处.
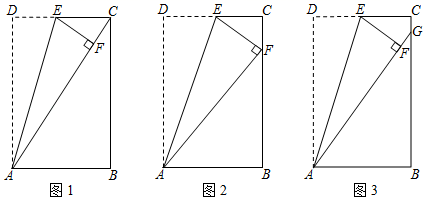 (1)、如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)、如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.(3)、如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.20. 在长方形中,点是中点,将沿折叠后得到对应的 , 将延长交直线于点 .
(1)、如图1,若点F落在对角线AC上,且∠BAC=54°,则∠DAE的度数为°.(2)、如图2,若点F落在边BC上,且AB=6,AD=10,求CE的长.(3)、如图3,若点E是CD的中点,AF的沿长线交BC于点G,且AB=6,AD=10,求CG的长.20. 在长方形中,点是中点,将沿折叠后得到对应的 , 将延长交直线于点 . (1)、如果点在长方形的内部,如图所示.
(1)、如果点在长方形的内部,如图所示.
①求证:;
②若 , , 求的长度.
(2)、如果点在长方形的外部,如图所示, , 请用含的代数式表示的值.
-