北师大版数学九(上)1.1菱形的性质与判定同步训练
试卷更新日期:2024-07-09 类型:同步测试
一、选择题
-
1. 如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,点E为垂足,连接DF,则∠CDF为( )
 A、80° B、70° C、65° D、60°2. 如图,要使成为菱形,则需添加的一个条件是( )
A、80° B、70° C、65° D、60°2. 如图,要使成为菱形,则需添加的一个条件是( ) A、 B、 C、 D、3. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )
A、 B、 C、 D、3. 如图,在菱形ABCD中,AC=6cm,BD=8cm,则菱形AB边上的高CE的长是( )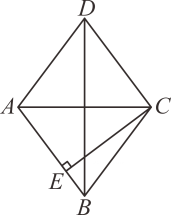 A、4.8cm B、9.6cm C、5cm D、10cm4. 如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )
A、4.8cm B、9.6cm C、5cm D、10cm4. 如图,菱形ABCD的周长为28,对角线AC,BD交于点O,E为AD的中点,则OE的长等于( )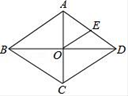 A、2 B、3.5 C、7 D、145. 下列关系中,是菱形的性质但不是平行四边形的性质的是( )A、对角线垂直 B、两组对边分别平行 C、对角线互相平分 D、两组对角分别相等6. 如图,在菱形 中, 是 边上的一点, 分别是 的中点,则线段 的长为( )
A、2 B、3.5 C、7 D、145. 下列关系中,是菱形的性质但不是平行四边形的性质的是( )A、对角线垂直 B、两组对边分别平行 C、对角线互相平分 D、两组对角分别相等6. 如图,在菱形 中, 是 边上的一点, 分别是 的中点,则线段 的长为( ) A、8 B、 C、4 D、7. 如图,已知菱形的周长为 , , 则对角线的长是( )
A、8 B、 C、4 D、7. 如图,已知菱形的周长为 , , 则对角线的长是( )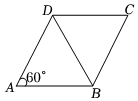 A、 B、 C、 D、8. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( )
A、 B、 C、 D、8. 已知菱形OABC在平面直角坐标系的位置如图所示,顶点 , , 点P是对角线OB上的一个动点, , 当最短时,点P的坐标为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如右图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个锐角为60°的菱形,剪口与折痕所成的角α的度数应为.
 10. 如图,连接四边形ABCD各边中点,得到四边形EFGH , 只要添加条件ACBD . 就能保证四边形EFGH是菱形.
10. 如图,连接四边形ABCD各边中点,得到四边形EFGH , 只要添加条件ACBD . 就能保证四边形EFGH是菱形. 11. 菱形的两条对角线长分别为和 , 则这个菱形的周长为 .12. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
11. 菱形的两条对角线长分别为和 , 则这个菱形的周长为 .12. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 . 13. 如图,在菱形中, , , 为边上一动点,将沿折叠为 , 为边上一点, , 则的最小值为 .
13. 如图,在菱形中, , , 为边上一动点,将沿折叠为 , 为边上一点, , 则的最小值为 .
三、作图题
-
14. 已知线段AC
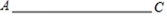 (1)、尺规作图:作菱形ABCD,使AC是菱形的一条对角线(保留作图痕迹,不要求写作法);(2)、若AC=8,BD=6,求菱形的边长.
(1)、尺规作图:作菱形ABCD,使AC是菱形的一条对角线(保留作图痕迹,不要求写作法);(2)、若AC=8,BD=6,求菱形的边长.四、解答题
-
15. 如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,过点A作AF∥BC交BE的延长线于F,BF交AC于G,连接CF.
 (1)、求证:EF=EB;(2)、若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论.16. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC , BD交于点O , AC平分∠BAD , 过点C作CE⊥AB交AB的延长线于点E , 连接OE .
(1)、求证:EF=EB;(2)、若∠BAC=90°,试判断四边形ADCF的形状,并证明你的结论.16. 如图,在四边形ABCD中,AB∥DC , AB=AD , 对角线AC , BD交于点O , AC平分∠BAD , 过点C作CE⊥AB交AB的延长线于点E , 连接OE .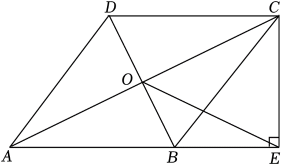 (1)、求证:四边形ABCD是菱形;(2)、若AB=10,BD=8,求OE的长.
(1)、求证:四边形ABCD是菱形;(2)、若AB=10,BD=8,求OE的长.五、实践探究题
-
17. 综合与实践
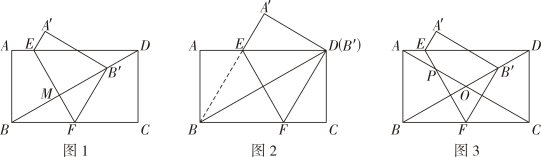
[问题情境]
如图1,小华将矩形纸片ABCD先沿对角线BD折叠,展开后再折叠,使点B落在对角线BD上,点B的对应点记为B',折痕与边AD,BC分别交于点E,F.
(1)、 [活动猜想]如图2,当点B'与点D重合时,四边形BEDF是哪种特殊的四边形?并给予证明.(2)、 [问题解决]如图1,当AB=4, AD=8,BF=3时,连结B'C,则B'C的长为(3)、 [深入探究]如图3,请直接写出AB与BC满足什么关系时,始终有A'B'与对角线AC平行?18. 课本再现思考
我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
可以发现并证明菱形的一个判定定理;
对角线互相垂直的平行四边形是菱形.
(1)、定理证明为了证明该定理,小明同学画出了图形(如图1),并写出了“已知”和“求证”,请你完成证明过程.
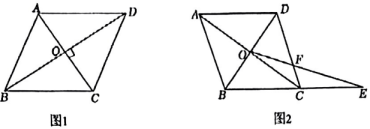
已知:在中,对角线 , 垂足为.
求证:是菱形.
(2)、知识应用如图2,在中,对角线AC和BD相交于点.求证:是菱形.
六、综合题
-

