新人教版（2024版）七年级上学期数学第一章质量进阶检测

试卷更新日期：2024-07-08 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列各组数中，互为相反数的是 $($ $)$

A、 $| - \frac{1}{3} |$ 和 $- \frac{1}{3}$ B、 $| - \frac{1}{3} |$ 和 $- 3$ C、 $| - \frac{1}{3} |$ 和 $\frac{1}{3}$ D、 $| - \frac{1}{3} |$ 和3

查看试题解析
2. 在数轴上距2.5有3.5个单位长度的点所表示的数是（）

A、6 B、-6 C、-1 D、-1或6

查看试题解析
3. 下列说法中：①﹣a一定是负数；②|﹣a|一定是正数；③有理数不是整数就是分数；④绝对值等于它本身的数是1；正确的说法有（）个

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，数轴上有三个点A，B，C，若点A，B表示的数互为相反数，且 $A B = 4$ ，则点C表示的数是（）

A、6 B、4 C、2 D、0

查看试题解析
5. 使等式 $| 6 + x | = | 6 | + | x |$ 成立的有理数 $x$ 是（）

A、任意一个整数 B、任意一个非负数 C、任意一个非正数 D、任意一个有理数

查看试题解析
6. 已知|a+2|+|b﹣1|＝0，则ab的值是（　　）

A、2 B、1 C、﹣2 D、﹣1

查看试题解析
7. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数．如图①表示的是（+2）+（-2），根据刘徽的这种表示法，可推算图②中所表示的算式为（　　）

A、（+3）+（+6） B、（-3）+（-6） C、（-3）+（+6） D、（+3）+（-6）

查看试题解析
8. 在数轴上，一动点 $A$ 向左移动 $2$ 个单位长度到达点 $B$ ，再向右移动 $5$ 个单位长度到达点 $C .$ 若点 $C$ 表示的数为 $1$ ，则点 $A$ 表示的数为（）

A、 $7$ B、 $3$ C、 $- 3$ D、 $- 2$

查看试题解析
9. 若 $a$ ， $b$ 互为相反数，则下列各对数中不是互为相反数的是（）

A、 $- 2 a$ 和 $- 2 b$ B、 $a + 1$ 和 $b + 1$ C、 $a + 1$ 和 $b - 1$ D、 $2 a$ 和 $2 b$

查看试题解析
10. 为检查四个篮球的质量，把超过标准质址的克数记为正数，不足标准质量的克数记为负数，结果如下表.其中质量最接近标准的是（）
篮球编号甲乙丙丁
与标准质量的差(g) +4 +7 -3 -8

A、甲 B、乙 C、丙 D、丁

查看试题解析

二、填空题（每题3分，共15分）

11. 在－42，＋0.01，π，0，120这5个数中，正有理数是．

查看试题解析
12. $- (+ \frac{1}{5})$ 的绝对值是。

查看试题解析
13. 若x为有理数，则 $5 - | x - 2 |$ 的最大值为

查看试题解析
14. 如图，数轴上点 $A$ 表示的数是2024，若 $O A = 2 O B$ ，则点 $B$ 表示的数是．

查看试题解析

三、解答题（（共3题，共24分））

15. 把下列各数填入相应的数集中：
$+ 1 \frac{2}{5}$ 、 $- 5 %$ 、 $200$ 、 $- 3$ 、 $6.8$ 、 $0$ 、 $- \frac{2}{15}$ 、 $0.12003407$ 、 $1$ 、 $- 43.555$ 、 $77 %$ 、 $- π$

(1)、非负整数集合：；

(2)、负数集合：；

(3)、正整数集合：；

(4)、负分数集合：．

查看试题解析
16. 某人用400元购买了8套儿童服装，准备以一定价格出售，如果每套儿童服装以55元的价格为标准，超出的记作正数，不足的记作负数，记录下：+2，﹣4，+2，+1，﹣2，﹣1，0，﹣2
当它卖它这8套儿童服装后是盈利还是亏损？盈利（亏损）多少钱？

查看试题解析
17. 体育课上，对初三（1）的学生进行了仰卧起坐的测试，以能做24个为标准，超过次数用正数来表示，不足的次数用负数来表示，其中10名女学生成绩如下：
5
－2
－1
3
0
10
0
7
－5
－1
这10名女生的达标率为多少？

查看试题解析

四、综合题（共5题，共51分）

18. 如图，快递员小刘要从公司点 $A$ 处出发，前往 $B$ ， $C$ ， $D$ 等地派送包裹，规定：向上向右走为正，向下向左走为负，并且行走方向顺序为先左右再上下.若从 $A$ 到 $B$ 记为： $A \to B (+ 1 ， + 4)$ ，从 $B$ 到 $A$ 记为： $B \to A (- 1 ， - 4)$ ，其中第一个数表示左右方向，第二个数表示上下方向.

(1)、A→C（，），B→D（，），C→D（，），

(2)、若快递员小刘的行走路线为 $A \to B \to C \to D$ ，请计算该快递员走过的路程；

(3)、若快递员小刘从 $A$ 处去某 $E$ 处的行走路线依次为 $(+ 2 ， + 2)$ ， $(+ 1 ， - 1)$ ， $(- 2 ， + 3)$ ， $(- 1 ， - 2)$ ，请在图中标出 $E$ 的位置.

查看试题解析
19. 快递员骑车从快递公司出发，先向北骑行 $200 m$ 到达A小区，继续向北骑行 $400 m$ 到达B小区，然后向南骑行 $1000 m$ 到达C小区，最后回到快递公司.

(1)、以快递公司为原点，以向南方向为正方向，用 $1 c m$ 表示 $100 m$ 画出数轴，并在该数轴上表示出 $A 、 B 、 C$ 三个小区的位置；

(2)、C小区离B小区有多远；

(3)、快递员一共骑行了多少千米？

查看试题解析
20. 如图所示，数轴上的一个单位长度表示2，观察下图，回答问题：

(1)、若点 $A$ 与点 $D$ 表示的数互为相反数，则点 $D$ 表示的数是多少？

(2)、若点 $B$ 与点 $F$ 表示的数互为相反数，则点 $D$ 表示的数的相反数是多少？

查看试题解析
21. 操作与探究：
已知在纸面上有数轴（如图），折叠纸面．
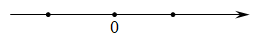
例如：若数轴上数3表示的点与数－3表示的点重合，则数轴上数－5表示的点与数5表示的点重合，根据你对例题的理解，解答下列问题：

(1)、若数轴上数2表示的点与－2表示的点重合，则数轴上数7表示的点与数表示的点重合．

(2)、若数轴上数－5表示的点与数1表示的点重合．
①则数轴上数3表示的点与数重合．
②若数轴上A，B两点之间的距离为10（A在B的左侧），并且A，B两点经折叠后重合，则A，B两点表示的数分别是，．

查看试题解析
22. 综合应用题：
$| m - n |$ 的几何意义是数轴上表示m的点与表示n的点之间的距离．

(1)、 $| x |$ 的几何意义是数轴上表示的点与之间的距离， $| x |$ $| x - 0 |$ ；（选填“>”“<”或“=”）

(2)、 $| 2 - 1 |$ 几何意义是数轴上表示2的点与表示1的点之间的距离，则 $| 2 - 1 | =$ ；

(3)、 $| x - 3 |$ 的几何意义是数轴上表示的点与表示的点之间的距离，若 $| x - 3 | = 1$ ，则 $x =$ ；

(4)、 $| x - (- 2) |$ 的几何意义是数轴上表示的点与表示的点之间的距离，若 $| x - (- 2) | = 2$ ，则 $x =$ ；

(5)、找出所有符合条件的整数x ，使得 $| x - (- 5) | + | x - 2 | = 7$ 这样的整数是．

查看试题解析

篮球编号	甲	乙	丙	丁
与标准质量的差(g)	+4	+7	-3	-8