人教版八年级上学期数学课时进阶测试12.3角平分线的性质（三阶）

试卷更新日期：2024-07-08 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在 $△ A B C$ 中， $∠ B A C$ 和 $∠ A B C$ 的平分线AE、BF相交于点O，AE交BC于B，BF交AC于F，过点O作 $O D ⊥ B C$ 于D，下列四个结论：① $∠ A O B = 90 ° + \frac{1}{2} ∠ C$ ；②当 $∠ C = 60 °$ 时， $A F + B E = A B$ ；③若 $O D = a$ ， $A B + B C + C A = 2 b$ ，则 $S_{△ A B C} = a h$ ．其中正确的是（）

A、①② B、②③ C、①②③ D、①③

查看试题解析
2. 如图，点P为定角∠AOB平分线上的一个定点，且∠MPN与∠AOB互补.若∠MPN在绕点P旋转的过程中，其两边分别与OA、OB相交于M、N两点，则以下结论：①PM=PN；②OM+ON的值不变；③MN的长不变；④四边形PMON的面积不变，其中，正确结论的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
3. 如图，在△ABC中，若分别以AB、AC为边作△ABD和△ACE，且∠DAB＝∠CAE＝α，AD＝AB，AC＝AE，DC、BE交于点P，连接AP，则∠APC的度数为（）

A、90°﹣ $\frac{1}{2}$ α B、90°+α C、90°﹣α D、90°+ $\frac{1}{2}$ α

查看试题解析
4. 如图 $A D$ 是 $△ A B C$ 的角平分线， $D E ⊥ A B$ 于E，点F，G分别是 $A B$ ， $A C$ 上的点，且 $D F = D G$ ， $△ A D G$ 与 $△ D E F$ 的面积分别是10和3，则 $△ A D F$ 的面积是（）

A、4 B、5 C、6 D、7

查看试题解析
5. 如图所示，在△ABC中，内角∠BAC与外角∠CBE的平分线相交于点P，BE＝BC，PB与CE交于点H，PG∥AD交BC于F，交AB于G，连接CP．下列结论：①∠ACB＝2∠APB；②S_△_PAC：S_△_PAB＝AC：AB；③BP垂直平分CE；④∠PCF＝∠CPF．其中，正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图， $△ A B C$ 中， $∠ A B C = 90 °$ ，点I为 $△ A B C$ 各内角平分线的交点，过I点作 $A C$ 的垂线，垂足为H，若 $B C = 3$ ， $A B = 4$ ， $A C = 5$ ，那么 $I H$ 的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析
7. 如图，∠ABD、∠ACD的角平分线交于点P，若∠A = 50°，∠D =10°，则∠P的度数为（）

A、15° B、20° C、25° D、30°

查看试题解析
8. 如图，在△ABC中，点E和F分别是AC、BC上一点，EF∥AB，∠BCA的平分线交AB于点D，∠MAC是△ABC的外角，若 $∠ M A C = α$ ， $∠ E F C = β$ ， $∠ A D C = γ$ ，则 $α$ 、 $β$ 、 $γ$ 三者间的数量关系是（）

A、 $β = α + γ$ B、 $β = 2 γ - α$ C、 $β = α + 2 γ$ D、 $β = 2 α - 2 γ$

查看试题解析

二、填空题

9. 如图，在 $△ A B C$ 中， $B D$ 平分 $∠ A B C$ ， $D A = D C$ ， $D E ⊥ A B$ 于点E ，若 $B C = 5$ ， $A E = 2$ ， $D E = 3$ ，则四边形 $A B C D$ 的面积是．

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ A = 60 ° (∠ A B C > ∠ A)$ ，角平分线 $B D$ 、 $C E$ 交于点 $O$ ， $O F ⊥ A B$ 于点 $F .$ 下列结论：
$① S_{△ B O C}$ ： $S_{△ B O E} = B C$ ： $B E$ ；
      $② ∠ E O F = ∠ A B C - ∠ A$ ；
      $③ B E + C D = B C$ ；
      $④ S_{四边形 B E D C} = 2 S_{△ B O C} + S_{△ E D O}$ ，
其中正确结论是．

查看试题解析
11. 如图，在 $Δ A B C$ 中， $∠ A B C$ 和 $∠ A C B$ 的平分线相交于点 $O$ ，过 $O$ 点作 $E F ∥ B C$ 交 $A B$ 于点 $E$ ，交 $A C$ 于点 $F$ ，过点 $O$ 作 $O D ⊥ A C$ 于 $D$ ，下列四个结论：① $E F = B E + C F$ ；② $∠ B O C = 90 ° - \frac{1}{2} ∠ A$ ；③点 $O$ 到 $Δ A B C$ 各边的距离相等；④设 $O D = m$ ， $A E + A F = n$ ，则 $S_{Δ A E F} = \frac{1}{2} m n$ ．其中正确的结论有（填写序号）．

查看试题解析
12. 如图，BA₁和CA₁分别是△ABC的内角平分线和外角平分线，BA₂是∠A₁BD的角平分线，CA₂是∠A₁CD的角平分线，BA₃是∠A₂BD的角平分线，CA₃是∠A₂CD的角平分线，若∠A=64°，则∠A= ， ∠A₃= ，若∠A=α，则∠A2018为。

查看试题解析

三、解答题

四、实践探究题

13. 八年级学生芳芳放学后去幼儿园接弟弟回家，姐弟俩双手相牵在幼儿园门口开心地旋转起来．芳芳突然想起某天数学活动课上老师提出的一个问题：如图，在△AOB和△EOF中，OA＝OB ， OE＝OF ，且∠1＝∠2，连接AE ， BF交于点M ．试猜想AE与BF的数量关系，并加以证明．

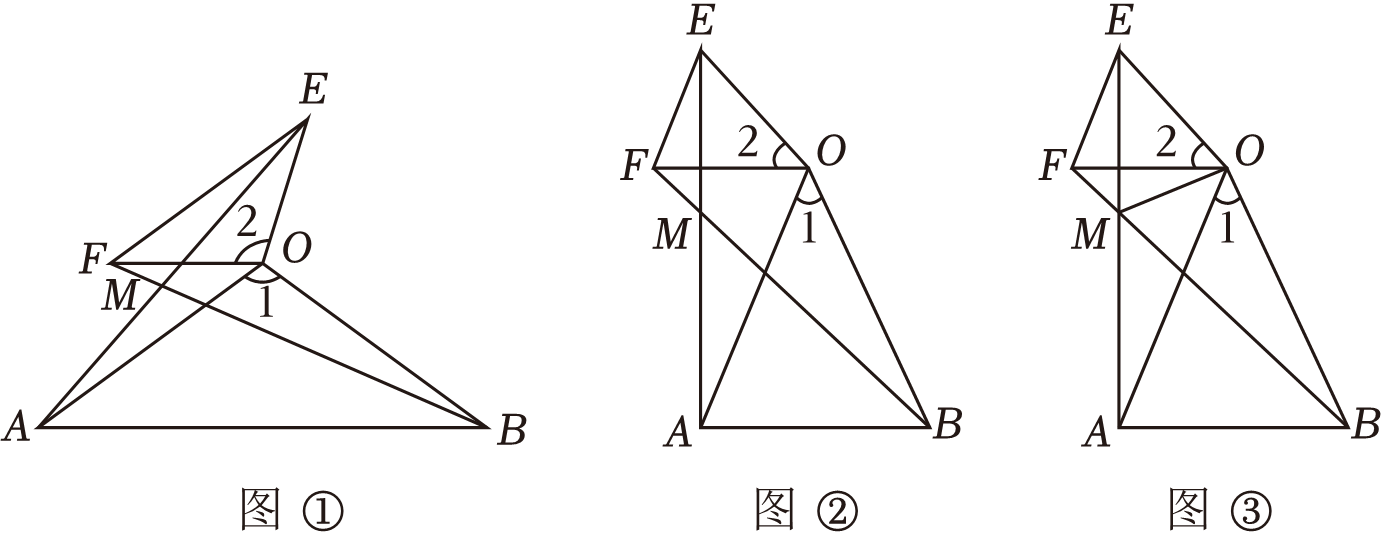(1)、独立思考：如图①，请解决老师提出的问题。

(2)、实践探究：如图②．当∠1＝45°时，∠AMB＝度；当∠OAB＝65°时，∠AMB＝度；

(3)、解决问题：如图③，连接OM ， MO平分∠BME吗？并加以说明．

查看试题解析