浙教版数学七升八暑假每天一测预习篇：全等三角形的实际应用
试卷更新日期：2024-07-07 类型：复习试卷
一、选择题（每题3分，共30分）
-
1. 如图，用螺丝钉将两根小棒的中点固定，利用全等三角形知识，测得的长就是锥形瓶内径的长，其中，判定和全等的方法是（ ）
A、 B、 C、 D、2. 如图，为了测量池塘两岸相对的A，B两点之间的距离，小明同学在池塘外取AB的垂线BF上两点C，D，BC=CD，再画出BF的垂线DE，使点E与A，C在同一条直线上，可得△ABC≌△EDC，从而DE=AB．判定△ABC≌△EDC的依据是（ ）
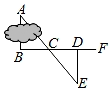A、ASA B、SAS C、AAS D、SSS3. 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中 ， ，测得 厘米， 厘米，则圆形容器的壁厚是（ ）
A、5厘米 B、6厘米 C、1厘米 D、0.5厘米4. 数学活动课上，小星制作了一个燕尾形的风筝如图， ， ， 他准备用刻度尺量和的长是否相等．
小英却说：“不用再测量，因为≌ ， 所以”
小英用到的判定三角形全等的方法是（ ）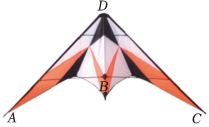
A、 B、 C、 D、5.如图所示，亮亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（ ）
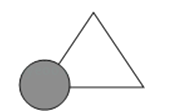A、SSS B、SAS C、AAS D、ASA6. 如图，一块三角形的玻璃被打碎成三块，小云同学现要配一块与原来形状完全相同的玻璃，则（ ）
A、只带①去 B、只带③去 C、只带②去 D、带②和③去7. 如图，小虎用10块高度都是的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板 ， 点C在上，点A和B分别与木墙的顶端重合，则两堵木墙之间的距离的长度为（ ）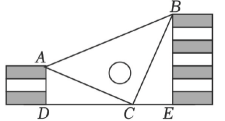
A、 B、 C、 D、8. 如图把两根钢条 ， 的中点连在一起，可以做成一个测量工件内槽宽的卡钳，此卡钳的工作原理是（ ）
A、SAS B、SSS C、ASA D、AAS9. 如图，为测量池塘两端A、B的距离，小康在池塘外一块平地上选取了一点O ， 连接AO ， BO ， 并分别延长AO ， BO到点C ， D ， 使得AO＝DO ， BO＝CO ， 连接CD ， 测得CD的长为165米，则池塘两端A ， B之间的距离为（ ）
A、160米 B、165米 C、170米 D、175米10. 某大学计划为新生配备如图①所示的折叠凳.图②是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计)，其中凳腿AB和CD的长相等，O是它们的中点.为了使折叠凳坐着舒适，厂家将撑开后的折叠凳宽度AD设计为30 cm，则由以上信息可推得CB的长度也为30 cm，依据是（ ）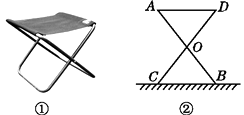
A、SAS B、ASA C、SSS D、AAS二、填空题（每题5分，共30分）
-
11. 如图，小明与小红玩跷跷板游戏，已知跷跷板的支点（即跷跷板的中点）至地面的距离是 ， 当小红从水平位置下降时，这时小明离地面的高度是 ．
12. 如图，把两根钢条AB ， CD的中点连在一起做成卡钳，已知AC的长度是6cm ， 则工件内槽的宽BD是 cm ．
13. 如图是雨伞在开合过程中某时刻的截面图，伞骨 ， 点D，E分别是AB，AC的中点，DM，EM是连接弹簧和伞骨的支架，且、已知弹簧M在向上滑动的过程中，总有 ， 其判定依据是.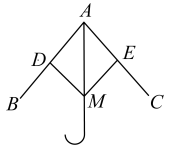
14. 工人师傅常用角尺平分一个任意角.作法：如图，在∠AOB的边OA，OB上分别取点M，N，使OM＝ON，移动角尺，使角尺两边相同的刻度分别与点M，N重合，得到∠AOB的平分线OP.作法中用到三角形全等的判定方法是.
15. 如图所示，要测量河岸相对的两点A、B之间的距离．已知AB垂直于河岸BF，在BF上取两点C、D，使CD＝CB，过点D作BF的垂线ED，使A、C、E在一条直线上，若ED＝90米，则AB的长是米．
16.如图，有两个长度相同的滑梯（即BC=EF），左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则∠ABC+∠DFE= 度．
三、解答题（共6题，共60分）
-
17. 小明和爸爸妈妈在公园里荡秋千如图，小明坐在秋千上的起始位置处，起始位置与地面垂直，两脚在地面上用力一蹬，妈妈在距地面米高的处接住他，然后用力一推，爸爸在处接住他若妈妈与爸爸到秋千起始位置的水平距离米，米，且 ， 求爸爸接住小明的位置距地面的高度．
18. 一次演习中，红军与蓝军在河边激战，蓝军在河北岸Ｑ处，如图，因不知河宽，红军很难瞄准蓝军，聪明的红军指挥官站在南岸Ｏ处调整好自己的帽子，使视线恰好擦过帽舌边沿看到蓝军兵营Ｑ处，然后后退到B点，这时他的视点恰好能落在O处，于是他下令测量他脚站的B处与O点之间的距离，并下令按这个距离炮轰蓝军兵营，红军能命中吗？说明理由．
19. 周末，小明和小玮去公园玩，他们发现一个人工湖，喜欢思考的小明对小玮说：“老师说，我们要用数学的眼光看世界，那么，你能用我们学过的数学知识测量出湖的宽度（以最宽处计算）吗？”小玮观察了一下，给出了如下测量方案．
如图，首先在湖两岸相对的地方选取两点两点之间的距离就是湖的宽度．要测量湖两岸相对的两点间的距离，可以在湖外取的垂线上的两点 ， 使 ， 再画出的垂线 ， 使点与点在同一条直线上．若想知道两点之间的距离，只需要测量出线段的长度即可．请你用学过的数学知识来说明小玮的做法是否正确．
20. 阿进在物理课上学习了发声物体的振动实验后，对其作了进一步的探究：如图，在一个支架的横杆点处用一根细绳悬挂一个小球 ， 小球可以自由摆动，表示小球静止时的位置.当阿进用发声物体靠近小球时，小球从摆到位置，此时过点作于点.当小球撰到位置时，与恰好垂直（图中的 ， ， ， 在同一平面上），过点作于点.
(1)、求证：；(2)、若阿进测得 ， ， 求的长.21. 【实际问题】在拓展训练过程中，小明和组员为了完成测河宽的任务，在不能过河测量又没有任何测量工具的情况下，设计出下面的方案：小明面向河对岸的方向站好，然后调整帽子，使视线通过帽檐正好落在河对岸一点；然后，他转过身，保持刚才的姿态，这时视线通过帽檐落在了自己所在岸的某一点上；接着，他用步测的方法量出自己与那个点的距离，这个距离就是河的宽度．
【数学建模】将小明看成一条线段 ， 河对岸一点为点 ， 自己所在岸的那个点为点 ， 示意图如图所示，请你根据示意图帮助小明同学将问题补充完整，并解释其中的道理．
如图，如果于点 ， ▲ ，那么 ．
【问题解决】说明AC=AD的理由．
22.八年级数学兴趣小组开展了测量学校教学楼高度的实践活动，测量方案如下表：
课题
测量学校教学楼高度
测量工具
测角仪、皮尺等
测量方案示意图
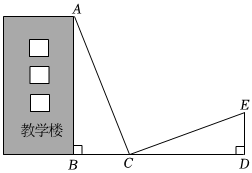
测量步骤
在教学楼外，选定一点；
测量教学楼顶点视线与地面夹角；
测的长度；
放置一根与长度相同的标杆 ， 垂直于地面；
测量标杆顶部视线与地面夹角 ．
测量数据
， ， ，
请你根据兴趣小组测量方案及数据，计算教学楼高度的值．