浙教版数学七升八暑假每天一测复习篇：真实情境下的平行线与平移
试卷更新日期：2024-07-07 类型：复习试卷
一、选择题（每题3分，共30分）
-
1. 如图，一条街道有两个拐角和 ， 测得 ， 则 ， 就可以知道 ， 其依据的定理是（ ）
A、同位角相等，两直线平行 B、同旁内角互补，两直线平行 C、内错角相等，两直线平行 D、平行于同一条直线的两直线平行2. 如图是小星探索两直线平行的条件时所用的学具，木条a，b、c在同一平面内，经测量 ， 要使木条 ， 则的度数应为（ ）
A、 B、 C、 D、3. 绿色出行，健康出行，你我同行.某市为了方便市民绿色出行，推出了共享单车服务.图1是某品牌共享单车放在水平地面的实物图，图2是其示意图，其中AB、CD都与地面平行，AM与BC平行，若 ， 则的度数为（ ）
A、 B、 C、 D、4. 近几年中学生近视的现象越来越严重，为保护视力，某公司推出了护眼灯，其侧面示意图（台灯底座高度忽略不计）如图所示，其中 ， ， 经使用发现，当时，台灯光线最佳．则此时的度数为（ ）
A、 B、 C、 D、5. 一辆汽车在公路上行驶，两次拐弯后，仍在原来的方向上平行行驶，那么两个拐弯的角度为（ ）A、先向左转60°，再向右转60° B、先向左转130°，再向左转50° C、先向左转50°，再向右转40° D、先向左转50°，再向左转40°6. 如图所示，光在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射，在空气中平行的两条入射光线，在水中的两条折射光线也是平行的．若水面和杯底互相平行，且 ， 则（ ）．
A、58° B、68° C、32° D、122°7. 如图在一块长14m、宽6m的长方形场地上，有一条弯曲的道路，其余的部分为绿化区，道路的左边线向右平移3m就是它的右边线，则绿化区的面积是（ ）
A、96m2 B、72m2 C、66m2 D、56m28. 2024年2月，“顺遂安康 龙腾盛世”长江主题灯光秀在武汉展演，两条笔直且平行的景观道、上放置A、B两盏激光灯（如图所示）.A灯发出的光线自按逆时针方向以每秒30°的速度旋转至便立即回转，并不断往返旋转；B灯发出的光线自按逆时针方向以每秒10°的速度旋转至就停止旋转.两灯不间断照射；B灯先转动2秒，A灯才开始转动，当两灯的光线互相平行时A灯旋转的时间是（ ）
A、1或6秒 B、8.5秒 C、3或6秒 D、1或8.5秒9. 如图，某住宅小区有一长方形地块，若要在长方形地块内修筑同样宽的两条道路，道路宽为 ， 余下部分绿化，则绿化的面积是（ ）
A、 B、 C、 D、10. 在后稷故里稷山县，有个流传三千多年的独特年俗，就是除夕日农民在自家院子地面上绘“麦囤”图案，以期风调雨顺，四时平安，五谷丰登，如图1是“麦囤”示意图，乐乐为了验证“麦囤”图案中一组线段是否平行，测量了其中一些角的度数，如图2，其中能说明的是（ ）
A、 ， B、 ， C、 ， D、 ，二、填空题（每题4分，共28分）
-
11. 如图，一个弯形管道ABCD的拐角 ， ， 这时说 ， 理由： ．
12. 如图，某酒店重新装修后，准备在大厅主楼梯上铺设红色地毯.已知这种地毯每平方米售价140元，主楼梯道宽 ， 其侧面如图所示，则购买地毯至少需要元.
13. 如图是超市里购物车的侧面示意图，扶手AB与车底CD平行，比大 ， 则的度数是.
14. 如图，有一块长为32 m、宽为24 m的长方形草坪，其中有两条直道将草坪分为四块，则分成的四块草坪的总面积是m2 ．
15. 一杆古秤在称物体时的状态如图所示，已知 ， 则的度数是.
16. 如图1 是我们常用的折叠式小刀，其刀柄的外形是一个长方形挖去一个小半圆，刀片的两条边缘线可看成两条平行的线段，转动刀片时会形成如图 2 所示的∠1 与∠2，则∠1 与∠2 的度数和为°.
17. 一副直角三角尺叠放如图1所示，现将的三角尺固定不动，将含的三角尺绕顶点A顺时针转动，使两块三角尺至少有一组边互相平行．如图2：当时， ． 则其它所有可能符合条件的度数为 ．
三、解答题（共7题，共62分）
-
18. 如图是一种躺椅及其简化结构示意图，扶手AB与底座CD都平行于地面，靠背DM与支架OE平行，前支架OE与后支架OF分别与CD交于点G和点D ， AB与DM交于点N ， 当前支架OE与后支架OF正好垂直，时，人躺着最舒服，求此时扶手AB与支架OE的夹角和扶手AB与靠背DM的夹角的度数．
19. 如图，一块不规则木料，只有一边成直线，木工师傅想在这块木料上截出一块有一组对边平行的木板，用“丁”字尺在处画了一条直线，然后又用“丁”字尺在处画了一条直线，画完后用锯沿锯开就截出了一块有一组对边平行的木料，请你用所学的几何知识说明这样做的道理．
20. 图①为北斗七星的位置图，图②将北斗七星分别标为 ， 将顺次首尾连接，若恰好经过点 ， 且 ， ， .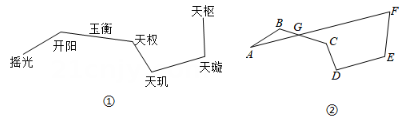
(1)、求的度数；(2)、计算的度数；(3)、连接与满足怎样数量关系时， ， 并说明理由.21. 如图，政府规划由西向东修一条公路.从A修至B后为了绕开村庄，改为沿南偏东25°方向修建BC段，在C处又改变方向修建CD段，测得∠BCD＝70°，在D处继续改变方向，朝与出发时相同的方向修至E.
(1)、补全施工路线示意图，求∠CDE的度数；(2)、原计划在AB的延长线上依次修建两个公交站M，N（均在CD右侧），连结DM和MN，求∠CDM与∠DMN的数量关系.22. 江夏文旅局计划“五·一”期间在中央公园举行大型灯光秀活动，沿湖两岸设置两座可以旋转的射灯，如图1，灯A射线从AM开始顺时针旋转至AN便立即回转，灯B射线从BP开始顺时针旋转至BQ便立即回转，两灯不停交叉照射，若灯A转动的速度是2度/秒，灯B转动的速度是1度/秒，假定湖两岸是平行的，即PQ//MN，且∠BAM：∠BAN=2：1.
(1)、填空：∠BAN=(2)、若灯B射线先转动30s，灯A射线才开始转动，在灯B射线到达BQ之前，灯A转动几秒，两灯的光束互相平行?(3)、如图2，若两灯同时转动，在灯A射线到达AN之前，假设射出的光束交点C，过点C作∠ACD交PQ于点D，且∠ACD=1200 ， 请探究：在转动过程中，∠BAC与∠BCD之间的数量关系是否发生变化?若不变，请求出其数量关系；若改变，请说明理由 .23. 在图①中，将线段向右平移1个单位得到线段 ， 从而得到封闭图形（即阴影部分）﹔在图②中，将折线向右平移1个单位得到折线 ， 从而得到封闭图形（即阴影部分）．
(1)、图①，图②图形中，除去阴影部分后，将剩余部分拼在一起就是如图③的图形，若剩余部分的面积分别是 ， （图①，图②长方形的长均为a个单位，宽均为b个单位），则 ， ， （填“＞”或“＝”或“＜”）﹔(2)、如图④，一块长方形场地由一条弯曲的小路和草地组成．这条弯曲的小路（即阴影部分）任何地方的水平宽度都是 ， 除去小路部分后，空白部分表示的草地的图形可拼在一起形成一个正方形，若这个正方形的面积是 ， 则原长方形场地的长和宽分别是多少m？(3)、如图⑤，一块长方形场地由两条弯曲的小路（阴影部分）和草地组成．竖直方向小路任何地方的水平宽度都是 ， 水平方向小路任何地方的竖直宽度都是 ． 除去小路部分后，空白部分表示草地的图形拼在一起形成一个长方形，且这个长方形的长是宽的2倍，面积是 ． 计划用不超过5200元的总费用将两条小路改铺成鹅卵石路面，若每路面的铺设费用（人工费材料费）约为200元，请问总预算5200元够吗？并说明理由．24. 【学科融合】物理学光的反射现象中，反射光线、入射光线和法线都在同一个平面内，反射光线和入射光线分别位于法线两侧，反射角等于入射角，这就是光的反射定律．
(1)、【理解运用】如图1，展示了光线反射定律，EF是镜面AB的垂线，一束光线m射到平面镜AB上，被AB反射后的光线为n ， 则入射光线m ， 反射光线n与垂线EF所夹的锐角 ， 则（填“”“”或“”）；
(2)、【尝试探究】学完光的反射定律，数学兴趣小组的同学想利用这个定律结合数学知识制作一个简易潜望镜，并画出了潜望镜的工作原理示意图，如图2，AB、CD是平行放置的两面平面镜，入射光线EF经过两次反射后，得到的反射光线GH ， 已知 ， ． 请问进入潜望镜的光线EF和离开潜望镜的光线GH是否平行，说明理由．
(3)、【拓展应用】如图3，AB、BC是两平面镜，入射光线FE经过两次反射后，反射光线GH与入射光线EF平行但方向相反．已知 ， ． 求的度数．