浙教版数学七升八暑假每天一测预习篇:勾股定理
试卷更新日期:2024-07-07 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 在下列四组数中,不是勾股数的一组数是( )A、a=15,b=8,c=17 B、a=9,b=12,c=15 C、a=7,b=24,c=25 D、a=3,b=5,c=72. 在锐角中, , , 高 , 则BC的长度为( )A、16 B、15 C、14 D、133. 下面四幅图中,不能证明勾股定理的是( )A、
 B、
B、 C、
C、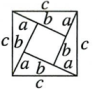 D、
D、 4. 如图,在等腰中,为的角平分线,若 , 则的长为( )
4. 如图,在等腰中,为的角平分线,若 , 则的长为( ) A、2 B、 C、4 D、5. 如图,在5×5的正方形网格中,从在格点上的点A , B , C , D中任取三点,所构成的三角形恰好是直角三角形的个数为( )
A、2 B、 C、4 D、5. 如图,在5×5的正方形网格中,从在格点上的点A , B , C , D中任取三点,所构成的三角形恰好是直角三角形的个数为( ) A、3 B、2 C、1 D、06. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 如图,圆柱的底面周长为6cm , AC是底面圆的直径,高BC=6cm , 点P是BC上一点且PC=
A、3 B、2 C、1 D、06. 满足下列条件的△ABC不是直角三角形的是( )A、BC=1,AC=2,AB= B、BC:AC:AB=3:4:5 C、∠A+∠B=∠C D、∠A:∠B:∠C=3:4:57. 如图,圆柱的底面周长为6cm , AC是底面圆的直径,高BC=6cm , 点P是BC上一点且PC= BC . 一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( )
BC . 一只蚂蚁从A点出发沿着圆柱体的表面爬行到点P的最短距离是( ) A、5cm B、cm C、cm D、7cm8. 如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米.若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( )
A、5cm B、cm C、cm D、7cm8. 如图,有一个绳索拉直的木马秋千,绳索AB的长度为5米.若将它往水平方向向前推进3米(即DE=3米),且绳索保持拉直的状态,则此时木马上升的高度为( ) A、1米 B、米 C、2米 D、4米9. 如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1 , S2 , S3和S4 . 若S1=2,S2=8,S4=3,则S3的值是( )
A、1米 B、米 C、2米 D、4米9. 如图,在四边形ABCD中,∠ABC=∠CDA=90°,分别以四边形ABCD的四条边为边长,向外作四个正方形,面积分别为S1 , S2 , S3和S4 . 若S1=2,S2=8,S4=3,则S3的值是( ) A、8 B、7 C、6 D、510. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”
A、8 B、7 C、6 D、510. 《九章算术》中有一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深,葭长各几何?”题意是:有一个池塘,其底面是边长为10尺的正方形,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B’(如图).则这根芦苇的长度是( )
 A、10尺 B、11尺 C、12尺 D、13尺
A、10尺 B、11尺 C、12尺 D、13尺二、填空题(每题4分,共24分)
-
11. 如图所示的一块地,∠ADC=90°,CD=3,AD=4,AB=13,BC=12,求这块地的面积为.
 12. 一艘轮船8:00从A港出发向西航行,10:00折向北航行,平均航速均为20千米/时,则11:30时该轮船离A港的距离为 .13. 如图,一架长2.5米的梯子斜立在一面竖直的墙上,梯子底端距离墙底0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端将向左滑动米.
12. 一艘轮船8:00从A港出发向西航行,10:00折向北航行,平均航速均为20千米/时,则11:30时该轮船离A港的距离为 .13. 如图,一架长2.5米的梯子斜立在一面竖直的墙上,梯子底端距离墙底0.7米,如果梯子的顶端沿墙下滑0.4米,那么梯子底端将向左滑动米. 14. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 , 较短直角边长为 , 若 , 大正方形的面积为 , 则小正方形的边长为 .
14. “赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为 , 较短直角边长为 , 若 , 大正方形的面积为 , 则小正方形的边长为 .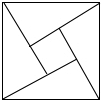 15. 下图是某公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走捷径AC,于是在草坪内走出了一条不该有的路AC,已知AB=40米,BC=30米,他们踩坏了米长的草坪,只为少走米的路.
15. 下图是某公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走捷径AC,于是在草坪内走出了一条不该有的路AC,已知AB=40米,BC=30米,他们踩坏了米长的草坪,只为少走米的路. 16. 如图是一个提供床底收纳支持的气压伸缩杆,除了AB是完全固定的钢架外,AD,BC,DE属于位置可变的定长钢架.如图1所示, , 伸缩杆PQ的两端分别固定在BC,CE两边上,其中.当伸缩杆PQ打开最大时,如图2所示,成 , 此时 , 则可变定长钢架CD的长度为.当伸缩杆完全收拢时, , 则此时床高(CD与AB之间的距离)为cm.
16. 如图是一个提供床底收纳支持的气压伸缩杆,除了AB是完全固定的钢架外,AD,BC,DE属于位置可变的定长钢架.如图1所示, , 伸缩杆PQ的两端分别固定在BC,CE两边上,其中.当伸缩杆PQ打开最大时,如图2所示,成 , 此时 , 则可变定长钢架CD的长度为.当伸缩杆完全收拢时, , 则此时床高(CD与AB之间的距离)为cm.
三、解答题
-
17. 用刻度尺和圆规作一条线段 ,使它的长度为cm.(保留作图痕迹)18. 如图,在△ABC中,AB=AC=5,BC=6,点D在AC边上,BD=AB .
 (1)、求△ABC的面积;(2)、求AD的长.19. 如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(1)、求△ABC的面积;(2)、求AD的长.19. 如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G. (1)、求证:EA=EG(2)、若BE=10,CD=3,G为CE中点,求AG的长.20. 在△ABC中,为AC边上一点,过点作交ED延长线于点.
(1)、求证:EA=EG(2)、若BE=10,CD=3,G为CE中点,求AG的长.20. 在△ABC中,为AC边上一点,过点作交ED延长线于点. (1)、求证:.(2)、连结BE,若是AC中点, , 求BE的长.21. 如图,在Rt△ABC中,∠ACB=90°,AC=BC , AE⊥CE ,BF⊥CE于点F .
(1)、求证:.(2)、连结BE,若是AC中点, , 求BE的长.21. 如图,在Rt△ABC中,∠ACB=90°,AC=BC , AE⊥CE ,BF⊥CE于点F . (1)、求证:△AEC≌△CFB;(2)、若AE=5,EF=7,求AB的长.22. 在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B,
(1)、求证:△AEC≌△CFB;(2)、若AE=5,EF=7,求AB的长.22. 在一款名为超级玛丽的游戏中,玛丽到达一个高为10米的高台A,利用旗杆顶部的绳索,划过90°到达与高台A水平距离为17米,高为3米的矮台B, (1)、求高台A比矮台B高多少米?
(1)、求高台A比矮台B高多少米?
(2)、求旗杆的高度OM;
(3)、玛丽在荡绳索过程中离地面的最低点的高度MN.
23. 为了测量学校旗杆的高度,八(1)班的两个数学研究小组设计了不同的方案,请结合下面表格的信息,完成任务问题.测量旗杆的高度
测量工具
测量角度的仪器、皮尺等
测量小组
第一小组
第二小组
测量方案示意图


设计方案及测量数据
在地面确定点C,并测得旗杆顶端A的仰角,即∠ACB=45°.
如图1,绳子垂直挂下来时,相比旗杆,测量多出的绳子长度FP为2米.如图2,绳子斜拉直后至末端点P位置,测量点P到地面的距离PD为1米,以及点P到旗杆AB的距离PE为9米.
(1)、任务一:判断分析第一小组要测旗杆AB的高度,只需要测量 的长度为线段并说明理由.
(2)、任务二:推理计算利用第二小组获得的数据,求旗杆的高度AB.
24. 定义:若三角形满足:两边的平方和与这两边乘积的差等于第三边的平方,则称这个三角形为“类勾股三角形”.如图1在中, , 则是“类勾股三角形”.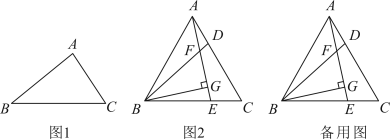 (1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.
(1)、等边三角形一定是“类勾股三角形”,是命题(填真或假).(2)、若中, , 且 , 若是“类勾股三角形”,求的度数.(3)、如图2,在等边三角形的边上各取一点 , , 且相交于点 , 是的高,若是“类勾股三角形”,且.①求证:.
②连结 , 若 , 那么线段能否构成一个“类勾股三角形”?若能,请证明;若不能,请说明理由.