浙教版数学七升八暑假每天一测预习篇：等腰（边）三角形的性质与判定

试卷更新日期：2024-07-07 类型：复习试卷

进入 出卷网 下载

一、选择题（每题3分，共30分）

  • 1. 下列命题中是真命题的是（　　）
    A、等边三角形一条边上的高线也是该条边上的中线 B、有一个角是60°的三角形是等边三角形 C、等腰三角形一定是锐角三角形 D、有一个角对应相等的两个等腰三角形全等

    查看试题解析

  • 2. 等腰三角形的一个角是80° ， 则它的底角是（ ）
    A、50° B、80° C、20°或80° D、50°或80°

    查看试题解析

  • 3. 下列条件中，不能判定△ABC是等腰三角形的是（     ）
    A、a=3，b=3，c=4 B、a︰b︰c=2︰3︰4 C、∠B=50°，∠C=80° D、∠A︰∠B︰∠C=1︰1︰2

    查看试题解析

  • 4. 如图，△ABC的面积为10cm2 ， BP平分∠ABC ， AP⊥BP ， 则△PBC的面积为（ ）

    A、5.5 B、6 C、5 D、4.5

    查看试题解析

  • 5. 在△ABC中，∠ABC=90° ， AB>BC ， 用无刻度的直尺和圆规在AC上找一点D ， 使△ABD为等腰三角形，下列作法不正确的是（ ）
    A、 B、 C、 D、

    查看试题解析

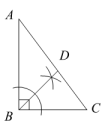  • 6. 如图，E是等边△ABC中AC边上的点，∠1=∠2，BE=CD，则△ADE的形状是（   ）

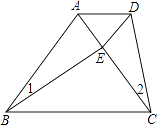    A、等腰三角形 B、等边三角形 C、不等边三角形 D、不能确定形状

    查看试题解析

  • 7. 如图，△ABC中，AB=6，AC=4，∠ABC和∠ACB的平分线交于点P，过点P作DE//BC分别交AB，AC于点D，E，则△ADE的周长为（    ）

    A、10 B、12 C、14 D、不能确定

    查看试题解析

  • 8. 如图，在“V”字形图形中，DE=DF ， BE=CF ， ∠D=60∘ ， CF//DE//AB ， BE//DF//AC ， 若要求出这个图形的周长，则需添加的一个条件是（ ）．

    A、BE的长 B、DE的长 C、AB的长 D、AB与BE的和

    查看试题解析

  • 9. 如图，上午8时，渔船从A处出发，以20海里/时的速度向正西方向航行，9时30分到达B处.从A处测得灯塔C在南偏西30°方向，距A处30海里处.则B处到灯塔C的距离是（   ）

    A、20海里 B、25海里 C、30海里 D、35海里

    查看试题解析

  • 10. 如图，已知∠AOB=120° ， 点D是∠AOB的平分线上的一上定点，点E ， F分别在射线OA和射线OB上，且∠EDF=60°.下列结论：①△DEF是等边三角形；②四边形DEOF的面积是一个定值；①当DE⊥OA时，△DEF的周长最小；④当DE∥OB时，DF也平行于OA.其中正确的个数是（    ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

二、填空题（每题4分，共24分）

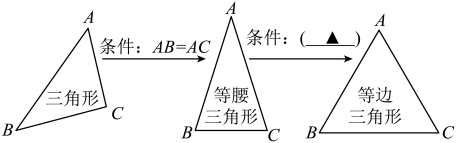
  • 11. 小明同学将几种三角形的关系整理如图，请帮他在括号内填上一个适当的条件是  ．

    查看试题解析

  • 12. 小明将两把完全相同的长方形直尺如图放置在∠AOB上，两把直尺的接触点为P ， 边OA与其中一把直尺边缘的交点为C ， 点C、P在这把直尺上的刻度读数分别是2、5，则OC的长度是 ．

    查看试题解析

  • 13. 如图，AE=AB ， ∠E=∠B，EF=BC ， 若∠EAB=52°，则∠EFA= ．

    查看试题解析

  • 14. 如图，Rt△ABC中，∠C=90°，AC=8，BC=6．有一动点P从点C开始沿C→B→A方向以2cm/s的速度运动到点A后停止运动，当运动时间为秒时，△ACP是等腰三角形．

    查看试题解析

  • 15. 如图，在△ABC中，BC＝8cm ， BP、CP分别是∠ABC和∠ACB的平分线，且PD∥AB ， PE∥AC，则△PDE的周长是cm ．

    查看试题解析

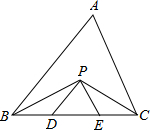  • 16. 由于木质衣架没有柔性，在挂置衣服的时候不太方便操作．小明设计了一种衣架，在使用时能轻易收拢，然后套进衣服后松开即可．如图1，衣架杆OA＝OB＝20cm，若衣架收拢时，∠AOB＝60°，如图2，则此时A，B两点之间的距离是cm．

    查看试题解析

三、作图题（共6分）

  • 17. 如图，已知点Q是直线AB上一动点（Q不与O重合)，∠POB=30°，请利用圆规和直尺，在图上找出所有的点Q，使得以P、O、Q为顶点的三角形是等腰三角形.

    查看试题解析

四、解答题（共7题，共60分）

  • 18. 如图，在△ABC与△DCB中，AC与BD交于点E ， 且∠A＝∠D ， AB＝DC ．

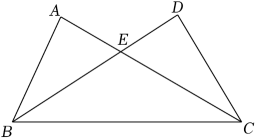    (1)、求证：△ABE≌△DCE；
    (2)、求证：∠EBC＝∠ECB ．

    查看试题解析

  • 19. 如图，在△ABC中，AB=AC ， E是△ABC内一点，F是BC上一点，∠EBF=∠E=60° ， AH平分∠BAC分别交EF、BC于点D、H ， 求∠EDA的度数.

    查看试题解析

  • 20. 如图，∠BCD＝90°，BC＝CD ， CD⊥AD ， AC、BD交于点E ， DA＝DE ， BN平分∠DBC ， 交AC于点M ， 交DC于点N ．

    (1)、求∠ACD的度数；
    (2)、求证：DB＝DA+DC；
    (3)、求证：AE＝2MN ．

    查看试题解析

  • 21. 如图，C为线段AE上一动点，（不与点A、E重合），在AE同侧分别作正△ABC和正△CDE ， AD与BE交于点O ， AD与BC交于点P ， BE与CD交于点Q ， 连接PQ ．

    (1)、求证：AD＝BE
    (2)、求证：△CQP是等边三角形
    (3)、若改变C的位置，其余条件都不变，点P恰好为BC的中点时，请问Q是否也为CD的中点，并说明理由．

    查看试题解析

  • 22. 如图， 在ΔABC中，AB=AC ， 点D ， E ， F分别在AB ， BC ， AC边上，且BE=CF ， BD=CE ．

    (1)、求证：ΔDEF是等腰三角形；
    (2)、当∠A=40°时， 求∠DEF的度数；
    (3)、若∠A=∠DEF ， 判断ΔDEF是何种三角形．

    查看试题解析

  • 23. 两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形．如图1，在“手拉手”图形中，AB＝AC，AD＝AE，∠BAC＝∠DAE，连结BD，CE，则△ABD≌△ACE．

    (1)、请证明图1的结论成立；
    (2)、如图2，△ABC和△AED是等边三角形，连接BD，EC交于点O，求∠BOC的度数；
    (3)、如图3，AB＝BC，∠ABC＝∠BDC＝60°，试探究∠A与∠C的数量关系．

    查看试题解析

  • 24. 概念学习

    规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”.

    从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”.

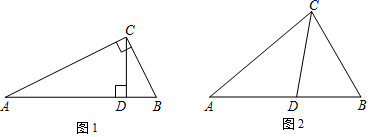    (1)、理解概念
    如图1，在Rt△ABC中，∠ACB=90° ， CD⊥AB ， 请写出图中两对“等角三角形”

    (2)、概念应用
    如图2，在△ABC中，CD为角平分线，∠A=40° ， ∠B=60°.

    求证：CD为△ABC的等角分割线.

    (3)、在△ABC中，∠A=42° ， CD是△ABC的等角分割线，直接写出∠ACB的度数.

    查看试题解析