浙教版数学七升八暑假每天一测预习篇：尺规作图

试卷更新日期：2024-07-07 类型：复习试卷

进入出卷网下载

一、选择题

1. 尺规作图的作图工具是（）

A、直尺、量角器 B、三角板、量角器 C、没有刻度的直尺和圆规 D、量角器

查看试题解析
2. 在下列各题中，属于尺规作图的是（）

A、用直尺画一工件边缘的垂线 B、用直尺和三角板画平行线 C、利用三角板画 $45 °$ 的角 D、用圆规在已知直线上截取一条线段等于已知线段

查看试题解析
3. 下列关于画图的语句正确的是（）

A、画直线AB=8cm B、画射线OA=8cm C、已知A，B，C三点，过这三点画一条直线 D、过直线AB外一点画一直线与AB平行

查看试题解析
4. 下列作图属于尺规作图的是（）

A、用量角器画出∠AOB的平分线OC B、借助直尺和圆规作∠AOB，使∠AOB=2∠α C、画线段AB=3cm D、用三角尺过点P作AB的垂线

查看试题解析
5. 用尺规作图，已知三边作三角形，用到的基本作图是（　　）

A、作一个角等于已知角 B、作已知直线的垂线 C、作一条线段等于已知线段 D、作角的平分线

查看试题解析
6. 如图，点C在∠AOB的边OB上，用尺规作出了∠BCN＝∠AOC ，作图痕迹中，弧FG是（　　）

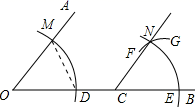A、以点C为圆心，OD为半径的弧 B、以点C为圆心，DM为半径的弧 C、以点E为圆心，OD为半径的弧 D、以点E为圆心，DM为半径的弧

查看试题解析
7. 如图（1）所示，已知线段 $a$ ， $∠ 1$ ，求作 $△ A B C$ ，使 $B C = a$ ， $∠ A B C = ∠ B C A = ∠ 1$ ，张蕾的作法如图（2）所示，则下列说法中一定正确的是（）

A、作 $△ A B C$ 的依据为ASA B、弧 $E F$ 是以 $A C$ 长为半径画的 C、弧 $M N$ 是以点 $A$ 为圆心， $a$ 为半径画的 D、弧 $G H$ 是以 $C P$ 长为半径画的

查看试题解析
8. 如图，已知线段a ， h作等腰△ABC ，使AB＝AC ，且BC＝a ， BC边上的高AD＝h ．张红的作法如下：
$(1)$ 作线段BC＝a；
$(2)$ 作线段BC的垂直平分线MN ， MN与BC相交于点D；
$(3)$ 在直线MN上截取线段h；
$(4)$ 连结AB ， AC ，则△ABC为所求的等腰三角形．
上述作法的四个步骤中，有错误的一步你认为是（）

A、 $(1)$ B、 $(2)$ C、 $(3)$ D、 $(4)$

查看试题解析
9. 下面出示的的尺规作图题，题中符号代表的内容正确的是（）
如图，已知∠AOB，求作：∠DEF，使∠DEF=∠AOB

作法：

⑴以①为圆心，任意长为半径画弧，分别交OA、OB于点P、Q；

⑵作射线EG，并以点E为圆心②长为半径画弧交EG于点D；

⑶以点D为圆心③长为半径画弧交（2）步中所画弧于点F；

⑷作④，∠DEF即为所求作的角．

A、①表示点E B、②表示PQ C、③表示OQ D、④表示射线EF

查看试题解析

二、填空题

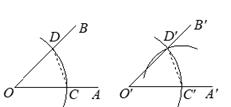
10. 如图，用尺规作图作“一个角等于已知角”的原理是：因为△D^′O^′C^′≌△DOC，所以∠D^′O^′C^′＝∠DOC。由这种作图方法得到的△D^′O^′C^′和△DOC全等的依据是（写出全等判定方法的简写）.

查看试题解析
11. 如图，若∠α=38°，根据尺规作图的痕迹，则∠AOB的度数为．

查看试题解析
12. 如图，△ABC是不等边三角形，DE＝BC，以D，E为两个顶点作位置不同的三角形，使所作的三角形与△ABC全等，这样的三角形最多可以画出个．

查看试题解析
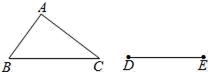13. 如图，AB∥CD，以点A为圆心，小于AC的长为半径画弧，分别交AB，AC于E，F两点；再分别以E，F为圆心，大于 $\frac{1}{2}$ EF的长为半径画弧，两弧交于点P，作射线AP，交CD于点M．若∠CMA=25°，则∠C的度数为.

查看试题解析

三、作图题

14. 尺规作图：（不写作法，保留作图痕迹）
已知： $∠ α$ 、 $∠ β$ ，线段 $a$ ．求作： $Δ A B C$ ，使 $∠ A B C = ∠ α$ ， $∠ B A C = ∠ β$ ， $A B = a$ ．

查看试题解析
15. 已知△ABC（如图），根据要求作图．
⑴用直尺和圆规作BC边上的中线．
⑵用直尺和圆规作∠C的平分线．
⑶作BC边上的高线．

查看试题解析
16. 如图，在 $△ A B C$ 中．

(1)、作 $∠ A B C$ 的平分线 $B D$ ．

(2)、作线段 $B D$ 的垂直平分线．（尺规作图，保留作图痕迹，不写作法）

查看试题解析
17. 如图，已知△ABC，请按下列要求用尺规作图．(保留作图痕迹，不写作法及证明)

(1)、作AB边的垂直平分线l，垂足为点D．

(2)、在(1)中所得直线l上，求作一点M，使点M到BC边所在直线的距离等于MD．

查看试题解析
18. 如图，校园有两条路OA和OB ，旁边有两块指示牌C ， D ，学校准备在附近安装一盏路灯，要求灯柱的位置P离两块指示牌一样远，并且到两条路的距离相等，请你帮助画出灯柱的位置P（要求尺规作图并保留作图痕迹）．

查看试题解析
19. 已知：两边及其夹角，线段 $a$ ， $c$ ， $∠ α$ .
求作： $△ A B C$ ，使 $B C = a$ ， $A B = c$ ，（用尺规作图，保留作图痕迹，不写作法）.

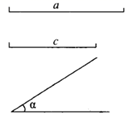
请你根据所学的知识，说明尺规作图作出 $∠ A B C = ∠ α$ ，用到的是三角形全等判定定理中的_▲_，作出的 $△ A B C$ 是唯一的，依据是三角形全等判定定理中的_▲_.

查看试题解析
20. 如图，在△ABC中，∠A＞∠B.

(1)、作边AB的垂直平分线DE，与AB，BC分别相交于点D，E（用尺规作图，保留作图痕迹，不要求写作法）；

(2)、在（1）的条件下，连接AE，若∠B＝50°，求∠AEC的度数.

查看试题解析
21. 如图，在Rt△ABC中，∠C＝90°，AC＜BC.

(1)、动手操作：要求尺规作图，不写作法，但保留作图痕迹.
①作出AB的垂直平分线MN，MN分别与AB交于点D，与BC交于点E.

②过点B作BF垂直于AE，垂足为F.

(2)、推理证明：求证AC＝BF.

查看试题解析
22. 解决下列两个问题：

(1)、如图1，在△ABC中，AB＝3，AC＝4，BC＝5．EF垂直且平分BC．点P在直线EF上，直接写出PA+PB的最小值，并在图中标出当PA+PB取最小值时点P的位置；
解：PA+PB的最小值为．

(2)、如图2．点M、N在∠BAC的内部，请在∠BAC的内部求作一点P，使得点P到∠BAC两边的距离相等，且使PM＝PN．（尺规作图，保留作图痕迹，无需证明）

查看试题解析