浙教版数学七升八暑假每天一测预习篇：角平分线与垂直平分线

试卷更新日期：2024-07-07 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图所示，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
2. 如图，OD平分 $∠ A O B ， D E ⊥ A O$ 于点 $E ， D E = 3 ， F$ 是射线OB上的任一点，则DF的长度不可能是（）

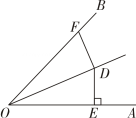A、2.8 B、3 C、4.2 D、5

查看试题解析
3.
如图，△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=8，DE=3，则△BCE的面积等于（　　）

A、11 B、8 C、12 D、3

查看试题解析
4. 如图，在△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以M，N为圆心，大于 $\frac{1}{2}$ MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（）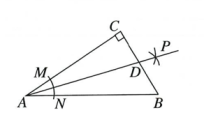

A、15 B、30 C、45 D、60

查看试题解析
5. 如图，在△ACB中，∠C=90°， AB的垂直平分线交AB、AC于点M、N，若AC=8，BC=4，则NC的长度为（）.

A、2 B、3 C、4 D、5

查看试题解析
6. 关于线段的垂直平分线有以下说法：
①一条线段的垂直平分线的垂足，也是这条线段的中点；
②线段的垂直平分线是一条直线；
③线段垂直平分线上的点到线段上任意一点的距离相等.
其中，正确的说法有（）

A、1个 B、2个 C、3个 D、0个

查看试题解析
7. 已知△ABC中，BC=6，AB、AC的垂直平分线分别交边BC于点M、N ，若MN=2，则△AMN的周长是（）

A、4 B、6 C、4或8 D、6或10

查看试题解析
8. 如图，在四边形ABCD中，AC平分∠BAD ， CE⊥AB于点E ， ∠ADC＋∠ABC＝180°，有下列结论：①CD＝CB；②AD＋AB＝2AE；③∠ACD＝∠BCE；④ $S_{∆ A B C}$ － $S_{∆ A D C}$ ＝2 $S_{∆ B E C}$ ，其中正确的是（）

A、② B、①②③ C、①②④ D、①②③④

查看试题解析
9. 如图，已知钝角 $△ A B C$ ，按照下列步骤作图：步骤1，以点 $C$ 为圆心，CA为半径作圆弧；步骤2，以点 $B$ 为圆心，BA为半径作圆弧，两圆弧交点记为D；步骤3：连结AD，交BC延长线于点 $H$ .根据作图过程得出以下结论： $A B = A D ；$ $B H ⊥ A D ；$ $S_{△ A B C} = B C \cdot A H ；$ $A C$ 平分 $∠ B A D$ .其中正确的是（）

A、 $A B = A D$ B、 $B H ⊥ A D$ C、 $S_{△ A B C} = B C \cdot A H$ D、AC平分 $∠ B A D$

查看试题解析
10. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EF $∥$ BC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC＝90° $+ \frac{1}{2}$ ∠A，②∠EBO $= \frac{1}{2}$ ∠AEF，③∠DOC+∠OCB＝90°，④设OD＝m，AE+AF＝n，则S_△AEF $= \frac{m n}{2}$ ．其中正确的结论有（）

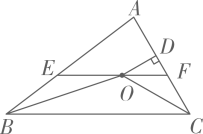A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为.

查看试题解析
12. 如图，在△ABC中，CD是边AB上的高，BE平分∠ABC，交CD于点E，BC＝5，若△BCE的面积为5，则ED的长为 .

查看试题解析
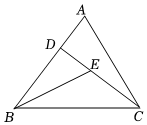13. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，以顶点A为圆心，适当长为半径画弧，分别交 $A C$ ， $A B$ 于点M，N，再分别以点M，N为圆心，大于 $\frac{1}{2} M N$ 的长为半径画弧，两弧交于点P，作射线 $A P$ ，交边 $B C$ 于点D，若 $C D = 3$ ， $A B = 12$ ，则 $△ A B D$ 的面积是．

查看试题解析
14. 如图， $△ A B C$ 中， $D E$ 是 $A B$ 的垂直平分线，交 $B C$ 于 $D$ ，交 $A B$ 于 $E$ ，已知 $A E = 1 c m$ ， $△ A C D$ 的周长为 $12 c m$ ，则 $△ A B C$ 的周长是 $c m$ ．

查看试题解析
15. 如图，直线CD是线段AB的垂直平分线，M是直线CD上一点．若线段MA=3，则线段MB= ，理由是

查看试题解析
16. 如图，BD垂直平分 $A G 于 D ， C E$ 垂直平分AF于 $E$ ，若 $B F = 1 ， F G = 3 ， G C = 2$ ，则 $△ A B C$ 的周长为.

查看试题解析

三、作图题（共2题，共14分）

17. 为了促进旅游发展，某地要在三条公路围成的一块平地上修建一个度假村．如图，要使度假村到三条公路的距离相等，它应修建在何处？在图中标出度假村的位置．

查看试题解析
18. 如图，在平面直角坐标系 $x O y$ 中，点 $A (0 ， 8)$ ，点 $B (6 ， 8)$ .

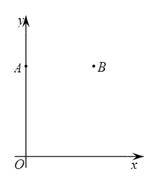(1)、只用直尺（没有刻度）和圆规，在第一象限内求作一个点P，使点P同时满足下列两个条件（要求保留作图痕迹，不必写出作法）；
①点P到A，B两点的距离相等；②点P到 $∠ x O y$ 的两边的距离相等.

(2)、在（1）作出点P后，直接写出点P的坐标.

查看试题解析

四、解答题（共7题，共52分）

19. 如图，AB与AC的垂直平分线相交于点O，若OA=2，BC=3，求△OBC的周长．

查看试题解析
20. 如图，
已知∠AOB= 90°，OM是∠AOB的平分线，将三角板的直角顶点P在射线OM上滑动，两直角边分别与OA，OB交于点C，D．

(1)、PC和PD的数量关系是

(2)、请证明(1)中得出的结论．

查看试题解析
21. 如图，在△ABC中，AB边的垂直平分线l₁交BC于点D ， AC边的垂直平分线l₂交BC于点E ， l₁与l₂相交于点O ．已知△ADE的周长为8cm．

(1)、求BC的长；

(2)、分别连接OA ， OB ， OC ，若△OBC的周长为20cm，求OA的长．

查看试题解析
22. 如图是一座斜拉桥的示意图，斜拉桥的拉杆BA，BC的两端点分别是A，C，支柱BO⊥AC，垂足为O，AO=CO．说明两条拉杆BA与BC的长度相等的理由．

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，E为CD的中点，连结AE，BE，延长AE交BC的延长线于点F．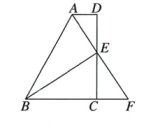

(1)、证明：FC=AD．

(2)、若AB= BC+AD，则BE⊥AF吗？为什么？

(3)、在(2)的条件下，若EC⊥BF，EC=3，则点E到AB的距离为

查看试题解析
24. 如图，在四边形 $A B C D$ 中，P为 $C D$ 边上的一点， $B C ∥ A D$ . $A P$ 、 $B P$ 分别是 $∠ B A D$ 、 $∠ A B C$ 的角平分线.

(1)、若 $∠ B A D = 70 °$ ，则 $∠ A B P$ 的度数为， $∠ A P B$ 的度数为；

(2)、求证： $A B = B C + A D$ ；

(3)、设 $B P = 3 a$ ， $A P = 4 a$ ，过点P作一条直线，分别与 $A D$ ， $B C$ 所在直线交于点E、F，若 $A B = E F$ ，直接写出 $A E$ 的长（用含a的代数式表示）

查看试题解析
25. 如图一，△ABC中，D是BC 的中点，过点D的直线GF交AC于点F，交AC的平行线BG于点G， DE⊥DF，交AB于点E，连结EG、EF.

(1)、求证：BG=CF；

(2)、如图二，当∠A=90°时，猜想BE，CF，EF的数量关系，并说明理由；

(3)、如图三，在(2)的条件下，当AB=AC时，求证ED=FD.

查看试题解析