浙教版数学七升八暑假每天一测预习篇：三角形全等的性质与判定-ASA和AAS

试卷更新日期：2024-07-07 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图 $A C$ 、 $B D$ 相交于点 $O$ ， $O A = O D$ ，若用“ $A S A$ ”证 $△ A B O ≌ △ D C O$ 还需（）

A、 $A B = D C$ B、 $O B = O C$ C、 $∠ A = ∠ D$ D、 $∠ A O B = ∠ D O C$

查看试题解析
2. 如图，小筧家里有一块三角形玻璃碎了，他带着残缺的玻璃去玻璃店配一块与原来相同的，请问师傅配出相同玻璃的依据是（）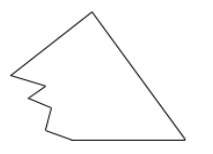

A、SSS B、SAS C、AAS D、ASA

查看试题解析
3. 如图， $△ A B C$ 的面积为 $7 c m^{2} ， B P$ 平分 $∠ A B C ， A P ⊥ B P$ 于点P，连结 $P C$ ，则 $△ P B C$ 的面积为（）

A、 $3 c m^{2}$ B、 $3.5 c m^{2}$ C、 $4 c m^{2}$ D、 $5 c m^{2}$

查看试题解析
4. 如图， $△ A B C$ 的面积为 $12 c m^{2}$ ， $A P$ 垂直于 $∠ A B C$ 的平分线 $B P$ 于 $P$ ，则 $△ P B C$ 的面积（）

A、 $9 c m^{2}$ B、 $8 c m^{2}$ C、 $6 c m^{2}$ D、 $5 c m^{2}$

查看试题解析
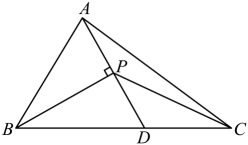5. 如图，在四边形ABCD中， $A D / / B C$ ，若∠DAB的角平分线AE交CD于E，连结BE，且BE平分∠ABC，则以下命题不正确的是（）

A、 $B C + A D = C D$ B、E为CD中点 C、 $∠ A E B = 90 °$ D、 $S_{△ A B E} = \frac{1}{2} S_{四边形 A B C D}$

查看试题解析
6. 如图，在△ABC中，点D为BC的中点，△AEF的边EF过点C，且AE=EF，AB∥EF，AD平分∠BAE，CE=3，AB=13，则CF=（）

A、10 B、8 C、7 D、6

查看试题解析
7. 下列说法中：

①如果两个三角形可以依据“AAS”来判定全等，那么一定也可以依据“ASA”来判定它们全等；

②如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；

③要判断两个三角形全等，给出的条件中至少要有一对边对应相等．

正确的是（　　）

A、①和② B、②和③ C、①和③ D、①②③

查看试题解析
8. 小李用7块长为8cm，宽为3cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AB＝BC，∠ABC＝90°），点B在DE上，点A和C分别与木墙的顶端重合，则两堵木墙之间的距离为（）

A、36 B、32 C、28 D、21

查看试题解析
9. 小丽与爸妈在公园里荡秋千．如图，小丽坐在秋千的起始位置A处，OA与地面垂直，两脚在地面上用力一蹬，妈妈在距地面1m高的B处接住她后用力一推，爸爸在C处接住她．若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m，∠BOC＝90°．爸爸在C处接住小丽时，小丽距离地面的高度是（）．

A、1m B、1.6m C、1.8m D、1.4m

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ B A C$ 和 $∠ A B C$ 的平分线 $A E$ ， $B F$ 相交于点O， $A E$ 交 $B C$ 于E， $B F$ 交 $A C$ 于F，过点O作 $O D ⊥ B C$ 于D，下列三个结论：① $∠ A O B = 90 ° + \frac{1}{2} ∠ C$ ；②当 $∠ C = 60 °$ 时， $A F + B E = A B$ ；③若 $O D = a$ ， $A B + B C + C A = 2 b$ ，则 $S_{△ A B C} = a b$ ．其中正确的个数是（）

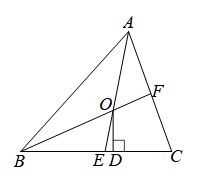A、1个 B、2个 C、3个 D、0个

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，已知AD∥BC．试添加一个条件：，能依据“ASA”来判定△ABC≌△CDA．（不添加其他字母及辅助线）

查看试题解析
12. 如图所示，∠E＝∠F＝90°，∠B＝∠C ， AE＝AF ．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN ．其中正确的结论是．（将你认为正确的结论的序号都填上）

查看试题解析
13. 如图，AB=CD，AD=BC，则图中全等三角形共有对．

查看试题解析
14. 如图， $∠ A C B = 90 °$ ， $A C = B C$ ， $A D ⊥ C E$ 于点 $D$ ， $B E ⊥ C E$ 于点 $E .$ 若 $A D = 2.5 c m$ ， $D E = 1.7 c m$ ，则 $B E =$ $c m$ ．

查看试题解析
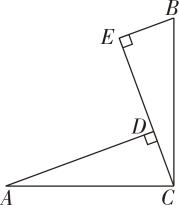15. 如图，点D是等腰 $R t △ A B C$ 的边BC上的一点，过点B作 $B E ⊥ A D$ 于点E，连接CE，若 $A E = 2$ ，则 $S_{△ A E C}$ 的值是．

查看试题解析
16. 如图，要测量池塘两岸相对的两点A ， B的距离，可以在池塘外取AB的垂线BF上的两点C ， D ，使BC＝CD ，再画出BF的垂线DE ，使E与A ， C在一条直线上．若想知道两点A ， B的距离，只需要测量出线段的长度即可．

查看试题解析

三、解答题（共6题，共44分）

17. 如图，已知 $△ A B C$ 和 $△ A D E$ ， $A B = A D$ ， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ D$ ， $A D$ 与 $B C$ 交于点 $P$ ，点 $C$ 在 $D E$ 上．求证： $B C = D E$ ；

查看试题解析
18. 已知：如图， $A C$ 与 $D B$ 相交于点 $O$ ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ 4$ ，求证： $A B = D C$ ．

查看试题解析
19. 如图，AC与BD相交于点O，且 $O A = O C$ ， $O B = O D$ .

(1)、求证： $A B // C D$ ；

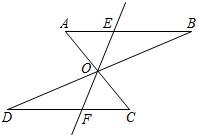(2)、直线EF过点O，分别交AB，CD于点E，F，试判断OE与OF是否相等，并说明理由.

查看试题解析
20. 如图，在 $△ A B C$ 中， $E$ 是 $A B$ 上一点， $A C$ 与 $D E$ 相交于点 $F$ ， $F$ 是 $A C$ 的中点， $A B$ ∥ $C D$ .

(1)、求证： $△ A E F ≌ △ C D F$ ；

(2)、若 $A B = 10 ， C D = 7$ ，求BE的长.

查看试题解析
21. 如图， $∠ A C B = 90 °$ ， $A C = B C$ ， $A D ⊥ M N$ ， $B E ⊥ M N$ ，垂足分别是 $D$ ， $E$ ．

(1)、求证： $△ A D C ≌ △ C E B$ ；

(2)、猜想线段 $A D$ ， $B E$ ， $D E$ 之间具有怎样的数量关系，并说明理由．

查看试题解析
22. 已知 $△ A B C$ 和 $△ A D E$ ，AB=AD， $∠ B A D = ∠ C A E$ ， $∠ B = ∠ D$ ，AD与BC交与点P，点C在DE上.

(1)、求证：BC=DE

(2)、若 $∠ B = 30 °$ ， $∠ A P C = 70 °$ ，
①求 $∠ E$ 的度数

②求证：CP=CE

查看试题解析

四、实践探究题（共2题，共22分）

23. 在△ABC中，点D在直线AB上，点E在平面内，点F在BC的延长线上，∠E=∠BDC，AE=CD，∠EAB+∠DCF=180°．

(1)、【问题解决】
如图1，若点D在边BA的延长线上，求证：AD+BC=BE；

(2)、【类比探究】
如图2，若点D在线段AB上，请直接写出线段AD、BC与BE之间存在怎样的数量关系；

(3)、【拓展延伸】
如图3若点D在线段AB的延长线上，请探究线段AD、BC与BE之间的数量关系，并证明．

查看试题解析
24.

(1)、某学习小组在探究三角形全等时，发现了下面这种典型的基本图形．如图1，已知：在△ABC中，∠BAC＝90°，AB＝AC ，直线l经过点A ， BD⊥直线l ， CE⊥直线l ，垂足分别为点D、E ．证明：DE＝BD+CE ．

(2)、组员小明想，如果三个角不是直角，那结论是否会成立呢？如图2，将（1）中的条件改为：在△ABC中，AB＝AC ， D ， A ， E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α ，其中α为任意锐角或钝角．请问结论DE＝BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3)、数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG ， AH是BC边上的高，延长HA交EG于点I ，求证：I是EG的中点．

查看试题解析