浙教版数学七升八暑假每天一测预习篇:三角形全等的性质与判定-SSS和SAS
试卷更新日期:2024-07-07 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 观察下列图案,其中与如图全等的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 如图,下列三角形中,与△ABC全等的是( )
2. 如图,下列三角形中,与△ABC全等的是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 下列命题属于假命题的是( )A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等4. 已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为( )
3. 下列命题属于假命题的是( )A、三个角对应相等的两个三角形全等 B、三边对应相等的两个三角形全等 C、全等三角形的对应边相等 D、全等三角形的面积相等4. 已知:如图△ABC≌△DCB,其中点A与点D,点B与点C分别是对应顶点,如果AB=2,AC=3,CB=4,那么DC的长为( )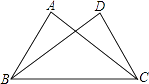 A、2 B、3 C、4 D、不确定5. 如图, , 其中 , , 则( )
A、2 B、3 C、4 D、不确定5. 如图, , 其中 , , 则( ) A、60° B、100° C、120° D、135°6. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS"还需要添加的一个条件是( )
A、60° B、100° C、120° D、135°6. 如图,已知点A,D,C,F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,依据“SSS"还需要添加的一个条件是( ) A、AD=CD B、AD=CF C、BC∥EF D、DC=CF7. 如图,AB=AD,BC=DC.若∠B=110°,∠BAD=90°,则∠BCA的度数为( )
A、AD=CD B、AD=CF C、BC∥EF D、DC=CF7. 如图,AB=AD,BC=DC.若∠B=110°,∠BAD=90°,则∠BCA的度数为( ) A、15° B、20° C、25° D、30°8. 如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( )
A、15° B、20° C、25° D、30°8. 如图,点E,F均在线段BC上,AB=DC,AE=DF,BF=CE.下列结论中,不一定成立的是( ) A、∠B=∠C B、AF∥DE C、AE=DE D、AB∥DC9. 若三角形的两边长分别为5和7,则第三边的中线长x的取值范围是( )A、 B、 C、 D、无法确定
A、∠B=∠C B、AF∥DE C、AE=DE D、AB∥DC9. 若三角形的两边长分别为5和7,则第三边的中线长x的取值范围是( )A、 B、 C、 D、无法确定二、填空题(每空3分,共27分)
-
10. 如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使 , 由和全等得到 . 那么判定其全等的依据是(用三个字母表示).
 11. 如图,在中, , , , 则的度数是 .
11. 如图,在中, , , , 则的度数是 .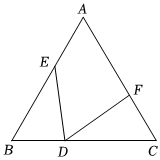 12. 如图,为的中线,延长至D,使 , 连接 , 已知 , , 则与的周长差是 .
12. 如图,为的中线,延长至D,使 , 连接 , 已知 , , 则与的周长差是 . 13. 尺规作角的平分线实际上是依据来判定两个三角形全等,从而证明作图方法是正确的.14. 如图,是AC上两点,且 , 欲证 , 可先运用等式的性质,证明 , 再用“SSS”证明 , 从而得到结论.
13. 尺规作角的平分线实际上是依据来判定两个三角形全等,从而证明作图方法是正确的.14. 如图,是AC上两点,且 , 欲证 , 可先运用等式的性质,证明 , 再用“SSS”证明 , 从而得到结论. 15. 如图,已知AB=AC,AD=AE,BD=EC,则图中有对全等三角形,它们是.
15. 如图,已知AB=AC,AD=AE,BD=EC,则图中有对全等三角形,它们是.
三、解答题(共8题,共63分)
-
16. 如图,OA=OC , OB=OD , ∠AOD=∠COB . 求证:AB=CD .
 17. 如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF.
17. 如图,AB=CB,BE=BF,∠1=∠2,证明:△ABE≌△CBF. 18. 如图,已知中, , AD是BC边上的中线,试猜想:
18. 如图,已知中, , AD是BC边上的中线,试猜想: (1)、与的大小关系;(2)、AD与BC的位置关系.并证明你的结论.19. 如图,为任意三角形,以边、为边分别向外作等边三角形和等边三角形 , 连接、并且相交于点 .
(1)、与的大小关系;(2)、AD与BC的位置关系.并证明你的结论.19. 如图,为任意三角形,以边、为边分别向外作等边三角形和等边三角形 , 连接、并且相交于点 . (1)、求证:;(2)、 .20. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点.
(1)、求证:;(2)、 .20. 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交BC于点D,DE⊥AB于点E,且E为AB的中点. (1)、求证:△ADE≌△BDE;(2)、求∠B的度数.21. 如图,是的边上的高,点E为上一点,且 .
(1)、求证:△ADE≌△BDE;(2)、求∠B的度数.21. 如图,是的边上的高,点E为上一点,且 . (1)、试说明;(2)、若 , 求的面积.
(1)、试说明;(2)、若 , 求的面积.

