(新)北师大版数学七上1.2从立体图形到平面图形 同步训练
试卷更新日期:2024-07-07 类型:同步测试
一、选择题
-
1. 用一个平面去截下列几何体,截面一定是圆的是( )A、
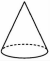 B、
B、 C、
C、 D、
D、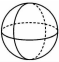 2. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字一面的相对面上的字是( )
2. 如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“我”字一面的相对面上的字是( )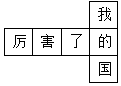 A、厉 B、害 C、了 D、国3. 如图是一个由5个相同的正方体组成的立体图形,从其正面看,得到的平面图形是( )
A、厉 B、害 C、了 D、国3. 如图是一个由5个相同的正方体组成的立体图形,从其正面看,得到的平面图形是( ) A、
A、 B、
B、 C、
C、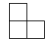 D、
D、 4. 如图是某几何体的从三个不同方向看到的图形,则这个几何体是( )
4. 如图是某几何体的从三个不同方向看到的图形,则这个几何体是( )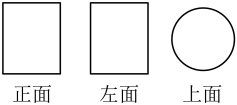 A、圆柱 B、正方体 C、球 D、圆锥5. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( )
A、圆柱 B、正方体 C、球 D、圆锥5. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( ) A、
A、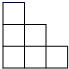 B、
B、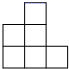 C、
C、 D、
D、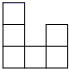 6. 如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( )
6. 如图所示的长方形(长为7,宽为4)硬纸板,剪掉阴影部分后,将剩余的部分沿虚线折叠,制作成底面为正方形的长方体箱子,则长方体箱子的体积为( ) A、22 B、5 C、7 D、117. 如图所示几何体的左视图是( )
A、22 B、5 C、7 D、117. 如图所示几何体的左视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 8. 图1、图2均是正方体,图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图,小敏同学经过研究得到如下结论:
8. 图1、图2均是正方体,图3是由一些大小相同的正方体搭成的几何体从正面看和左面看得到的形状图,小敏同学经过研究得到如下结论:⑴若将图1中正方体的表面沿某些棱剪开,展成一个平面图形,需要剪开7条棱;
⑵用一个平面从不同方向去截图1中的正方体,得到的截面可能是三角形、四边形、五边形或六边形;
⑶用一个平面去截图1中的正方体得到图2,截面三角形ABC中∠ABC=45°;
⑷如图3,要搭成该几何体的正方体的个数最少是a,最多是b,则a+b=19
其中正确结论的个数有( )
 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图,四边形ABCD去掉∠C后,剩下的新图形是边形.
 10. 将如图所示的长方体用过的平面切割,得到的两个几何体是 .
10. 将如图所示的长方体用过的平面切割,得到的两个几何体是 . 11. 由大小相同的小正方体搭成一个几何体,若搭成的几何体的左视图和俯视图如图所示,则所需小正方体的最少个数为 .
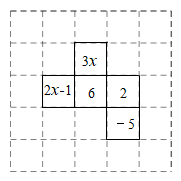
11. 由大小相同的小正方体搭成一个几何体,若搭成的几何体的左视图和俯视图如图所示,则所需小正方体的最少个数为 . 12. 正方体木块的六个面分别标有数字1,2,3,4,5,6,如图是从不同方向观察这个正方体木块看到的数字情况,数字1和5对面的数字的和是 .
12. 正方体木块的六个面分别标有数字1,2,3,4,5,6,如图是从不同方向观察这个正方体木块看到的数字情况,数字1和5对面的数字的和是 . 13. 用若干个大小相同的小立方体搭一个几何体,使得从正面和上面看到的这个几何体的形状如图所示,假设搭这个几何体至少需要个立方体.
13. 用若干个大小相同的小立方体搭一个几何体,使得从正面和上面看到的这个几何体的形状如图所示,假设搭这个几何体至少需要个立方体.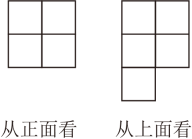
三、作图题
-
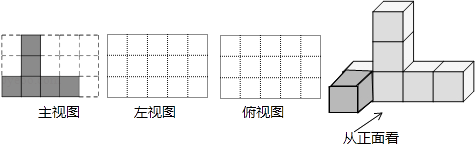
14. 5个棱长为1的正方体组成如图所示的几何体.
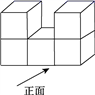 (1)、该几何体的体积是(立方单位),表面积是(平方单位);(2)、画出该几何体的主视图和左视图.15. 如图是由棱长为的6块小正方体组成的简单几何体:
(1)、该几何体的体积是(立方单位),表面积是(平方单位);(2)、画出该几何体的主视图和左视图.15. 如图是由棱长为的6块小正方体组成的简单几何体: (1)、请在方格中画出该几何体的三个视图;(2)、如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加块小正方体;(3)、添加最多的小正方体后,该几何体的表面积为 .
(1)、请在方格中画出该几何体的三个视图;(2)、如果在这个几何体上再添加一些小正方体,并保持主视图和左视图不变,最多可以再添加块小正方体;(3)、添加最多的小正方体后,该几何体的表面积为 .四、解答题
-
16. 在学习《展开与折叠》这一课时,老师让同学们将准备好的正方体或长方体沿某些棱剪开,展开成平面图形.其中,阿中同学不小心多剪了一条棱,把一个长方体纸盒剪成了图①、图②两部分.根据你所学的知识,回答下列问题:
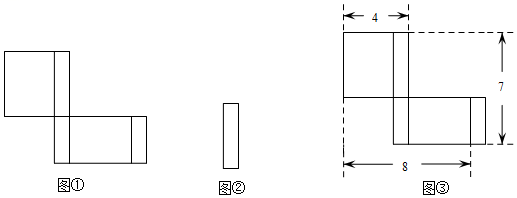 (1)、阿中总共剪开了几条棱?(2)、现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);(3)、已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.17. 如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图).
(1)、阿中总共剪开了几条棱?(2)、现在阿中想将剪断的图②重新粘贴到图①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,他有几种粘贴方法?请在图①上画出粘贴后的图形(画出一种即可);(3)、已知图③是阿中剪开的图①的某些数据,求这个长方体纸盒的体积.17. 如图是小强用八块相同的小立方体搭成的一个几何体,从正面、左面和上面观察这个几何体,请你在下面相应的位置分别画出你所看到的几何体的形状图(在答题卡上画完图后请用黑色签字笔描图).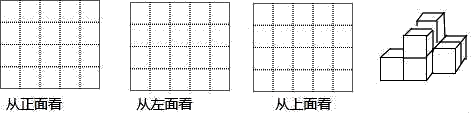
五、实践探究题
-
18. 【问题情境】小明所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.
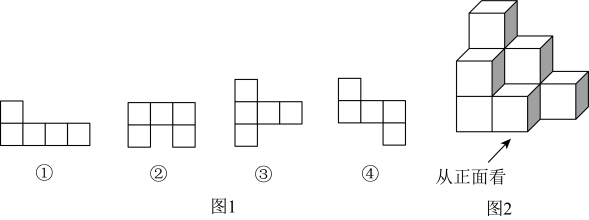
【操作探究】
(1)、图1中的第个图形经过折叠不能围成无盖正方体纸盒(填序号).(2)、小圣所在的综合实践小组把折叠成9个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的表面积;
②要保持从上面看到的平面图形不变,最多可以拿走小正方体的个数是 ▲ .
六、综合题