浙教版数学七升八暑假每天一测预习篇：定义、命题与证明

试卷更新日期：2024-07-07 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列语句中是命题的是（）

A、作 $∠ A O B$ 的平分线 $O C$ B、美丽的大自然 C、同位角相等 D、你吃饭了吗

查看试题解析
2. 下列语句中，不是命题的是（　　）

A、两点确定一条直线 B、垂线段最短 C、作角A的平分线 D、内错角相等

查看试题解析
3. 下列语句是命题的是（）

A、把 $△ A B C$ 绕着点A旋转 $60 °$ B、三角形三个角的平分线的交点是这个三角形的重心吗？ C、作 $△ A B C$ 的 $A B$ 边上的高 D、三角形一个外角大于这个三角形的任何一个内角

查看试题解析
4. 下列命题中，是真命题的是（　　）

A、内错角相等 B、64的立方根是8 C、三角形的内角和等于180° D、相等的两个角是对顶角

查看试题解析
5. 下列命题为真命题的是（）

A、同旁内角互补 B、若 $a^{2} = b^{2}$ ，则 $a = b$ C、在同一平面内，垂直同一条直线的两条直线互相平行 D、如果一个整数能被3整除，那么这个数也能被6整除

查看试题解析
6. 下列命题中，是真命题的是（）

A、如果 $a c > b c$ ，那么 $a > b$ B、9的立方根是3 C、有一个角是 $60 °$ 的三角形是等边三角形 D、16的算术平方根是4

查看试题解析
7. 在下面四个命题是真命题的个数有（）

(1)、互相垂直的两条线段一定相交；（2）有且只有一条直线垂直于已知直线；（3）两条直线被第三条直线所截，同位角相等；（4）从直线外一点到这条直线的垂线段，叫做这点到这条直线的距离．

A、3个 B、2个 C、1个 D、0个

查看试题解析
8. 下列命题中，假命题的个数有（）
①实数与数轴上的点一一对应；②无限小数就是无理数；③一个数的算术平方根是它本身，这个数是1；④三角形的一个外角大于任何一个和它不相邻的内角；⑤两条直线被第三条直线所截，同旁内角互补．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图， $D E / / B C ， B E$ 平分 $∠ A B C$ ，求证： $∠ 1 =$ $∠ 3$ .以下是排乱的证明过程：
① $∵ D E / / B C$ (已知)，
② $∵ B E$ 平分 $∠ A B C$ (已知)，
③ $∴ ∠ 1 = ∠ 2$ (角平分线的定义)，
④ $∴ ∠ 2 = ∠ 3$ (两直线平行，同位角相等)，
⑤ $∴ ∠ 1 = ∠ 3$ (等量代换).
证明步㵵顺序正确的是（）

A、③ $\to$ ② $\to$ ① $\to$ ④ $\to$ ⑤ B、① $\to$ ④ $\to$ ② $\to$ ③ $\to$ ⑤ C、① $\to$ ③ $\to$ ④ $\to$ ② $\to$ ⑤ D、① $\to$ ④ $\to$ ③ $\to$ ② $\to$ ⑤

查看试题解析

10. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容，则回答正确的是（）

已知：如图， $B D ⊥ A C$ ， $E F ⊥ A C$ ，垂足为D ， F ， $∠ 1 + ∠ 2 = 180 °$ ．

求证： $D G ∥ B C$ ．

证明：∵ $B D ⊥ A C$ ， $E F ⊥ A C$ ，

∴ $∠ B D C =$ ◎ $= 90 °$ ，

∴ $B D ∥ E F$ （同位角相等，两直线平行），

∴ $∠ 2 +$ @ $= 180 °$ （两直线平行，同旁内角互补）．

又∵ $∠ 1 + ∠ 2 = 180 °$ ，

∴ $∠ 1 =$ ▲ （同角的补角相等），

∴ $D G ∥ B C$ （ ※ 相等，两直线平行）．

A、◎代表

∠ E F D

B、@代表

∠ C E F

C、▲代表

∠ D B C

D、※代表同位角

查看试题解析

二、填空题（每题4分，共24分）

11. 把命题“同角的补角相等”改写为“如果……，那么……”的形式，如果那么．

查看试题解析
12. 把命题“全等三角形的对应高线相等”改写成“如果……，那么……．的形式：．

查看试题解析
13. 命题“若 $| a | > | b |$ ，则 $a > b$ ”是命题．（填“真”或“假”）

查看试题解析
14. 命题“如果 $a = b$ ，那么 $a^{2} = b^{2}$ ”是命题．（填“真”或“假”）

查看试题解析
15. 命题“面积相等的三角形是全等三角形”是命题． $（$ 填“真”或“假” $）$

查看试题解析
16. 证明命题“三角形的外角大于任何一个和它不相邻的角”按题意画出图形，请结合图形，写出“已知”和“求证”。
已知：如图，是的外角．
求证：，

查看试题解析

三、解答题（共9题，共66分）

17. 如图，AB，CD，BE，CF被BC所截．在下面三个论断中，请选择其中的两个作为条件，另一个为结论，组成一个真命题，并用推理的方法说明它是真命题．
①AB⊥BC，CD⊥BC；②BE∥CF ；③∠ABE=∠DCF．
条件：
结论：
推理过程：

查看试题解析
18. 如图，在△ABC中，E是CA延长线上一点，AD⊥BC于D，EG⊥BC于G，∠E=∠1．
求证：∠1=∠2．

查看试题解析
19. 如图，∠ABC的两边分别平行于∠DEF的两边，且∠ABC=25°．

(1)、图1中∠1= ，图2中∠2=.

(2)、观察∠1，∠2分别与∠ABC有怎样的数量关系，请你对此归纳出一个真命题．

查看试题解析
20. 证明命题“两条平行线被第三条直线所截，一对内错角的角平分线互相平行”是真命题．

查看试题解析
21. 观察下面三个三角形的形状，找出它们的共同特征，并对有这些共同特征的三角形下一个定义．

查看试题解析
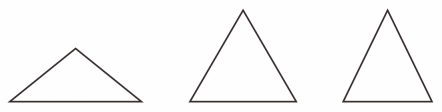22. 如图，在△ABC中，AD⊥BC于点D，AE平分∠BAC．完成下列问题：

(1)、若∠B=68°，∠C=34°，求∠DAE的度数．

(2)、若∠B>∠C，试猜想∠DAE与∠B-∠C有何关系，并证明．

查看试题解析
23. 已知：如图， $A B / / D C$ ， $A C$ 和 $B D$ 相交于点 $O$ ， $E$ 是 $C D$ 上一点， $F$ 是 $O D$ 上一点，
且 $∠ 1 = ∠ A$ ．

(1)、求证： $F E / / O C$ ；

(2)、若 $∠ B F E = 110 °$ ， $∠ 1 = 60 °$ ，求 $∠ B$ 的度数．

查看试题解析
24. 如图，
①AB∥CD，②BE平分∠ABD；③∠1+∠2=90°，④DE平分∠BDC．

(1)、请以其中三个为条件，第四个为结论，写出一个命题．

(2)、判断这个命题是否为真命题，并说明理由．

查看试题解析

25. 阅读与思考

提出命题	如果一个角的两边与另一角的两边互相垂直，那么这两个角相等
⑴判断真假	这个命题是 ▲ 命题（填“真”或“假”）
⑵求证过程	①若是真命题，请证明； ②若是假命题，请举出一个反例（要求画出相应的图形，并用文字语言或符号语言叙述所举的反例）
⑶结论应用	若两个角的两边互相垂直，且一个角比另一个角的2倍少 $30 °$ ，则这两个角的度数分别为 ▲ （直接写出结果）

查看试题解析