浙教版数学七升八暑假每天一测预习篇:认识三角形
试卷更新日期:2024-07-07 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 在△ABC中,∠A=15°,∠B=65°,则△ABC的形状是( )A、等边三角形 B、锐角三角形 C、直角三角形 D、钝角三角形2. 三角形按边长关系,可分为( )A、等腰三角形,等边三角形 B、直角三角形,不等边三角形 C、等腰三角形,不等边三角形 D、直角三角形,等腰三角形3. 下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、 , , B、 , , C、 , , D、 , ,4. 在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为( )A、40° B、45° C、50° D、60°5. 一副三角板,按如图所示叠放在一起,则图中的度数是( )
 A、 B、 C、 D、6. 在中, , 则边上的高的长度是( ).A、5 B、 C、 D、7. 如图,的中线交于点 , 若阴影部分的面积是 , 则的面积是( )
A、 B、 C、 D、6. 在中, , 则边上的高的长度是( ).A、5 B、 C、 D、7. 如图,的中线交于点 , 若阴影部分的面积是 , 则的面积是( ) A、 B、 C、 D、8. 下面四个图形中,线段能表示的高的是( )A、
A、 B、 C、 D、8. 下面四个图形中,线段能表示的高的是( )A、 B、
B、 C、
C、 D、
D、 9. 如图, , , 分别是的高、角平分线、中线,则下列结论错误的是( )
9. 如图, , , 分别是的高、角平分线、中线,则下列结论错误的是( ) A、 B、 C、 D、10. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个
A、 B、 C、 D、10. 用12根等长的火柴棒拼成一个三角形,火柴棒不允许剩余,重叠和折断,则能摆出不同的三角形的个数是( )A、1个 B、2个 C、3个 D、4个二、填空题(每题4分,共24分)
-
11. 如图,以BE为边的三角形有 个.
 12. 一个三角形两边长分别为3和8,第三边长为奇数,则第三边长为 .13. 已知,在中, , 则是三角形.14. 如图,在中, , , , 则的度数是
12. 一个三角形两边长分别为3和8,第三边长为奇数,则第三边长为 .13. 已知,在中, , 则是三角形.14. 如图,在中, , , , 则的度数是 15. 如图,是的中线,若的面积是 , 则的面积是 .
15. 如图,是的中线,若的面积是 , 则的面积是 . 16. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= , △APE的面积等于6.
16. 如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以每秒2cm的速度沿A→C运动,然后以1cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t= , △APE的面积等于6.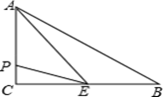
三、作图题(共6分)
-
17. 仅用无刻度的直尺和圆规完成下列作图.

⑴作△ABC的角平分线CD.
⑵作△ABC的高线AE.
四、解答题(共6题,共51分)
-
18.
张爷爷家有一块三角形的花圃ABC,张爷爷准备将其分成面积相等的四部分,分别种上不同的花卉.请你帮张爷爷设计三种不同的方案.
 19. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.
19. 如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数.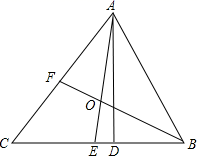 20. 如图,已知 , 分别是边上的高和中线,若 , , , .
20. 如图,已知 , 分别是边上的高和中线,若 , , , . (1)、求的长度.(2)、求的面积.21. 如图,已知锐角三角形ABC,若∠ABC=40°,∠ACB=70°,点D,E分别在边AB,AC上,CD与BE交于点H.
(1)、求的长度.(2)、求的面积.21. 如图,已知锐角三角形ABC,若∠ABC=40°,∠ACB=70°,点D,E分别在边AB,AC上,CD与BE交于点H. (1)、若BE⊥AC,CD⊥AB,求∠BHC的度数.(2)、若BE,CD分别平分∠ABC和∠ACB,求∠BHC的度数.22. 已知a , b , c是三角形的三边长,化简:|a+c﹣b|﹣|a+b+c|+|2b+c|.23. 小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.(1)、请用a表示第三条边长.(2)、问第一条边长可以为7m吗?请说明理由.
(1)、若BE⊥AC,CD⊥AB,求∠BHC的度数.(2)、若BE,CD分别平分∠ABC和∠ACB,求∠BHC的度数.22. 已知a , b , c是三角形的三边长,化简:|a+c﹣b|﹣|a+b+c|+|2b+c|.23. 小王准备用一段长30m的篱笆围成一个三角形形状的场地,用于饲养家兔,已知第一条边长为am,由于受地势限制,第二条边长只能是第一条边长的2倍多2m.(1)、请用a表示第三条边长.(2)、问第一条边长可以为7m吗?请说明理由.五、实践探究题(共9分)
-
24. 阅读与理解:
三角形的中线的性质:三角形的中线等分三角形的面积,即如图1,AD是△ABC中BC边上的中线,则S△ABD=S△ACD=S△ABC .

操作与探索:
在图2至图4中,△ABC的面积为a.
(1)、如图2,延长△ABC的边BC到点D,使CD=BC,连结DA.若△ACD的面积为S1 , 则S1= . (用含a的代数式表示).(2)、如图3,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连结DE.若△DEC的面积为S2 , 则S2=(用含a的代数式表示).(3)、在图3的基础上延长AB到点F,使BF=AB,连结FD,FE,得到△DEF(如图4).若图4中△DEF的面积为S3 , 则S3=(用含a的代数式表示).
-