浙江省衢州市金衢十二校2024年中考模拟数学试卷

试卷更新日期：2024-07-04 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. 2024的相反数是（）

A、 $\frac{1}{2024}$ B、2024 C、 $- \frac{1}{2024}$ D、-2024

查看试题解析
2. 下列计算正确的是（）

A、 $a^{8} \div a^{2} = a^{4}$ B、 $a + a^{2} = a^{3}$ C、 ${(a^{2})}^{3} = a^{5}$ D、 $a^{2} \cdot a^{3} = a^{5}$

查看试题解析
3. 新时代我国教育事业取得了历史性成就，目前我国已建成世界上规模最大的教育体系，教育现代化发展总体水平跨入世界中上国家行列，其中高等教育在学总规模达到4430万人，处于高等教育普及化阶段.4430万用科学记数法表示为（）

A、 $443 \times 1 0^{5}$ B、 $4.43 \times 1 0^{7}$ C、 $4.43 \times 1 0^{8}$ D、 $0.443 \times 1 0^{8}$

查看试题解析
4. 二次根式 $\sqrt{x - 2}$ 中字母x的取值范围是（）

A、 $x > 2$ B、 $x \neq 2$ C、 $x \geq 2$ D、 $x \leq 2$

查看试题解析
5. 下列几何体中，其主视图和左视图不同的是（）

A、 B、 C、 D、

查看试题解析
6. 一副三角板有两个直角三角形，如图叠放在一起，则 $∠ α$ 的度数是（）

A、 $6 5^{°}$ B、 $7 5^{°}$ C、 $12 0^{°}$ D、 $13 5^{°}$

查看试题解析
7. 在如图所示的电路中，随机闭合开关 $S_{1}$ ， $S_{2}$ ， $S_{3}$ 中的两个，能让红灯发光的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{1}{2}$

查看试题解析
8. 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何?”意思是：用一根绳子去量一根木条，绳子还剩余4.5尺；将绳子对折再量木条，木条剩余1尺，问木条长多少尺?如果设木条长x尺，绳子长y尺，那么可列方程组为（）

A、 ${\begin{cases} y = x + 4.5 \\ 0.5 y = x - 1 \end{cases}$ B、 ${\begin{cases} y = x + 4.5 \\ y = 2 x - 1 \end{cases}$ C、 ${\begin{cases} y = x - 4.5 \\ 0.5 y = x + 1 \end{cases}$ D、 ${\begin{cases} y = x - 4.5 \\ y = 2 x - 1 \end{cases}$

查看试题解析
9. 已知抛物线 $y = a (x - m) (x - n)$ 经过点 $A (1, p), B (7, p), C (8, p - 1)$ ，其中m、n、p为互不相等的实数，则下面判断不正确的是（）

A、 $a < 0$ B、对称轴为直线 $x = 4$ C、 $m + n = 8$ D、 $p < 0$

查看试题解析
10. 由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示．点 $O$ 是正方形ABCD的中心，连接AO并延长交BE于点 $F$ ，连接DF，记 $△ A B F$ 的面积为 $S$ ，正方形ABCD的面积为 $S_{1}$ ．若 $A F = k A D$ ，则 $\frac{S}{S_{1}}$ 的值为（）

A、 $\frac{1}{3} k$ B、 $\frac{\sqrt{2}}{4} k$ C、 $\frac{1}{4} k$ D、 $\frac{\sqrt{2}}{3} k$

查看试题解析

二、填空题（本大题共6小题，每小题3分，共18分）

11. 分解因式： $x^{2} - 3 x =$ .

查看试题解析
12. 已知圆锥的母线长为10，底面圆半径为5，则此圆锥的侧面积为．

查看试题解析
13. 如图，在数轴上点M，N分别表示数 $1, - 3 x + 2$ ，则 $x$ 的取值范围是．

查看试题解析
14. 如图，有一个侧面为梯形的容器，高为 $8 c m$ ，内部倒入高为 $6 c m$ 的水．将一根长为 $18 c m$ 的吸管如图放置，若有 $2 c m$ 露出容器外，则吸管在水中部分的长度为 $c m$ ．

查看试题解析
15. 如图，在菱形ABCD中， $∠ A B C = 12 0^{°}$ ，将菱形折叠，使点 $A$ 恰好落在对角线BD上的点 $G$ 处（不与B，D重合），折痕为EF，若 $D G = 2, B G = 4$ ，则点 $E$ 到BD的距离为．

查看试题解析
16. 如图， $⊙ O$ 的弦BC垂直平分半径OA，点 $E$ 是弦 $B C$ 上一点，且 $B E > C E$ ，连接AE并延长交 $⊙ O$ 于点 $D$ ，连结OD，OE，设 $D E = n O E$ ．

(1)、当点 $E$ 是AD中点时， $\overset{⌢}{C D}$ 的度数为 $°$ ；

(2)、连接AC，当 $\frac{A C}{D E} = m$ 时，则 $m$ 与 $n$ 之间的关系式为．

查看试题解析

三、解答题（本大题共8小题，共66分）

17. 计算： $| - 3 | + {(\frac{1}{3})}^{- 1} + \sqrt{12} - 2 s i n 6 0^{°}$ ．

查看试题解析
18. 对于实数a，b，定义新运算“ $\oplus$ ”，规定如下： $a \oplus b = (a + b - 1)^{2} - 2 a b$ 如 $1 \oplus 2 = (1 + 2 - 1)^{2} - 2 1 2 = 0$

(1)、求 $3 \oplus 5$ 的值；

(2)、若 $x$ 为某一个实数，记 $x \oplus 3$ 的值为 $m, 1 \oplus (2 - x)$ 的值为 $n$ ，请你判断 $m - n$ 的值是否与 $x$ 的取值有关?并给出证明．

查看试题解析
19. 如图，在矩形 $A B C D$ 中， $A B = 4, B C = 2$ ，连结 $A C$ ．

(1)、尺规作图：作菱形 $A E C F$ ，使得点E ， F分别在边 $A B, C D$ 上（保留作图痕迹，不写作法）．

(2)、求（1）中所作的菱形 $A E C F$ 的边长．

查看试题解析

20. 为了加强心理健康教育，某校组织八年级

(1) (2)

两班学生进行了心理健康常识测试，已知两班学生人数相同，根据测试成绩绘制了如下所示的统计图．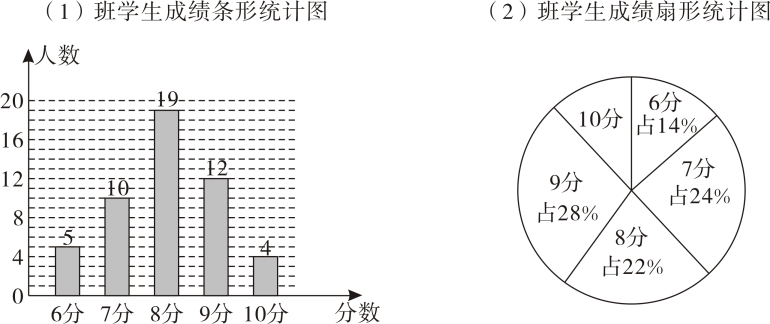

(1)、请确定下表中

a

，

b

，

c

的值：

统计量	平均数	众数	中位数
$(1)$ 班	$8$	$8$	$c$
$(2)$ 班	$a$	$b$	$8$

$a =$ 分， $b =$ 分， $c =$ 分；

(2)、根据上表中各种统计量，说明哪个班的成绩更突出一些．

查看试题解析

21. 如图所示，直线 $y = - \frac{1}{2} x + 4$ 与双曲线 $y = \frac{k}{x} (x > 0)$ 交于 $A (2, n), B$ 两点，与 $y$ 轴交于点 $D$ ．

(1)、求k，n的值：

(2)、求 $△ A O B$ 的面积；

(3)、请结合上述两个函数的图象，请直接写出 $\frac{6}{x} + \frac{1}{2} x > 4$ 的解集．

查看试题解析
22. 在 $△ A B C$ 中， $∠ A C B = 9 0^{°}$ ，点 $D$ 为BC上一点且 $B D = 2 C D$ ，连接AD．E，F分别为AD、AB的中点，连结DF，EF，EC，CF，ED与FC交于点 $O$ ．

(1)、求证：四边形ECDF是平行四边形；

(2)、若 $O F = 5, t a n ∠ C F E = \frac{4}{3}$ ，求AD的长.

查看试题解析
23. 【综合与实践】
某乒乓球馆使用发球机进行辅助训练，出球口A位于桌面BC左上方，桌面BC的长为 $2.74 m$ ．过点 $A$ 作 $O A ⊥ B C$ ，垂足为 $O, O B = 0.03 m$ ，以点 $O$ 为原点，以直线BC为 $x$ 轴，OA所在直线为 $y$ 轴，建立平面直角坐标系，如图所示，从出球口 $A$ 发出的乒乓球运动路线为抛物线的一部分 $L$ ，设乒兵球与出球口 $A$ 的水平距离为 $x (m)$ ，到桌面的高度为 $y (m)$ ，在桌面上的落点为 $D$ ，经测试，得到如下部分数据：
$x (m)$
0
0.5
1
1.5
2
…
$y (m)$
0.25
0.4
0.45
0.4
0.25
…

(1)、当 $x =$ ▲ $m$ 时，乒乓球达到最大高度；求出 $y$ 与 $x$ 之间的函数关系式；

(2)、桌面正中间位置安装的球网GH的高度为 $0.15 m$ ，问乒乓球位于球网正上方时，乒乓球到球网顶端 $H$ 的距离约为多少?（结果保留两位小数）

(3)、乒乓球落在点 $D$ 后随即弹起，沿抛物线 $L^{^{'}} : y = - \frac{\sqrt{3}}{2} (x - p) (x - 3.5)$ 的路线运动，小明拿球拍EF与桌面夹角为 $6 0^{°}$ 接球，球拍击球面的中心线EF长为 $0.16 m$ ，下沿 $E$ 在 $x$ 轴上，假设抛物线 $L$ ， $L^{^{'}}$ 与EF在同一平面内，且乒乓球落在EF上（含端点，点 $E$ 在点 $C$ 右侧），直接写出：
① $p =$ ；
②球拍到桌边的距离CE的取值范围．

查看试题解析
24. 如图1，在 $⊙ O$ 中，直径AB垂直弦CD，连结AC、AD，弦CG平分 $∠ A C D$ 分别交AB、AD于点E，F，AG与CD的延长线交于点 $H$ ．

(1)、求证： $△ A C G ~ △ A H C$ ；

(2)、如图1，当 $H G = H D$ 时，求 $\frac{A G}{G H}$ ；

(3)、如图2，当 $E F = F G$ 时，求 $\frac{S_{△ A E F}}{S_{△A C H}}$ ．

查看试题解析

$x (m)$	0	0.5	1	1.5	2	…
$y (m)$	0.25	0.4	0.45	0.4	0.25	…