浙江杭州市丰潭中学2024年九年级下学期数学二模（5月）

试卷更新日期：2024-07-04 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题,每小题3分,共30分)

1. 如果水位升高3m时水位变化记作 $+ 3 m$ ，那么水位下降3m时记作（）

A、+3m B、 $- 3 m$ C、0m D、 $\pm 3 m$

查看试题解析
2. 中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划，“一带一路”地区覆盖总人口约为4500000000人，将这个数用科学记数法表示为（）

A、 $0.45 \times 1 0^{10}$ B、 $4.5 \times 1 0^{10}$ C、 $4.5 \times 1 0^{9}$ D、 $4.5 \times 1 0^{8}$

查看试题解析
3. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{5}$ B、 ${(a^{2})}^{4} = a^{6}$ C、 $a^{8} \div a^{2} = a^{4}$ D、 $a^{5} + a^{5} = 2 a^{10}$

查看试题解析
4. 一个不等式的解在数轴上表示如图，则这个不等式可以是（）

A、 $x + 2 > 0$ B、 $x - 2 < 0$ C、 $2 x \geq 4$ D、 $2 - x < 0$

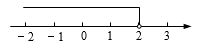查看试题解析
5. 将分别标有数字2，3，x的三个球放入不透明的袋中，这些球除所标的数字外都相同，搅匀后任意摸出一个球．若摸出球上的数字小于7是必然事件，则x的值可以是（）

A、11 B、9 C、7 D、5

查看试题解析
6. 在平面直角坐标系中，点 $P (m - 2, 2 m)$ 在第三象限，则下列 $m$ 的值可能是（）

A、-1 B、0 C、2 D、4

查看试题解析
7. 《儿章算术》是人类科学史上应用数学的“算经之首”，书中记载：今有三人共车，二车空；二人共车，九人步.问：人与车各几何?其大意是：若3人坐一辆车，则两辆车是空的；若2人坐一辆车，则9人需要步行.问：人与车各多少?设有 $x$ 人， $y$ 辆车，则符合题意的方程组是

A、 ${\begin{array}{l} x = 3 (y + 2) \\ x = 2 y - 9 \end{array}$ B、 ${\begin{array}{l} x = 3 (y + 2) \\ x - 9 = 2 y \end{array}$ C、 ${\begin{array}{l} x = 3 (y - 2) \\ x = 2 y - 9 \end{array}$ D、 ${\begin{array}{l} x = 3 (y - 2) \\ x - 9 = 2 y \end{array}$

查看试题解析
8. 如图.将菱形ABCD绕点A逆时针旋转 $∠ α$ 得到菱形 $A B^{'} C^{'} D^{'}$ ， $∠ B = ∠ β$ .当AC平分 $∠ B^{'} A C^{'}$ 时， $∠ α$ 与 $∠ β$ 满足的数量关系是（）

A、 $∠ α = 2 ∠ β$ B、 $2 ∠ α = 3 ∠ β$ C、 $4 ∠ α + ∠ β = 180 °$ D、 $3 ∠ α + 2 ∠ β = 180 °$

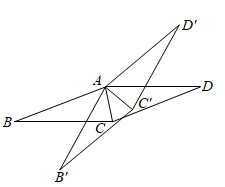查看试题解析
9. 将Rt $△ A B C$ 的直角边BC、斜边AB按如图方式构造正方形BCED和正方形ABFG，在正方形ABFG内部构造矩形ABHI使得边IH刚好过点 $D$ ，则已知哪条线段的长度就可以求出图中阴影部分的面积（）

A、AB B、AC C、BD D、FH

查看试题解析
10. 已知二次函数 $y = a x^{2} + 2 x + 1$ （a为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq x_{0}$ 的任意一个x的值，都有 $- 3 \leq y \leq 3$ ，则 $x_{0}$ 的最大值为（）

A、 $2 \sqrt{3} - 2$ B、 $2 \sqrt{3} + 2$ C、 $2 \sqrt{5} + 2$ D、 $2 \sqrt{5} - 2$

查看试题解析

二、填空题(本大题有6个小题,每小题3分,共18分)

11. 若 $\sqrt{x - 3}$ 在实数范围内有意义，则实数 $x$ 的取值范围是.

查看试题解析
12. 如图，直线 $a / / b$ ，直线 $c$ 分别交a，b于点A，C，点 $B$ 在直线 $b$ 上， $A B ⊥ A C$ ，若 $∠ 1 =$ $13 0^{°}$ ，则 $∠ 2$ 的度数是.

查看试题解析
13. 如图为某农科所在相同条件下做玉米种子发芽实验结果统计图，某位顾客购进这种玉米种子10千克，那么能发芽的种子质量大约为千克.

查看试题解析
14. 如图，在半径为 $\sqrt{2}$ 的圆形纸片中，剪一个圆心角为 $9 0^{°}$ 的最大扇形(阴影部分)，将此扇形围成一个无底的圆锥(不计接头)，则圆锥底面半径为.

查看试题解析
15. 在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点.如图，在 $6 \times 6$ 的正方形网格图形ABCD中，M，N分别是AB，BC上的格点， $B M = 4, B N = 2$ .若点 $P$ 是这个网格图形中的格点，连结PM，PN，则所有满足 $∠ M P N = 4 5^{°}$ 的 $△ P M N$ 中，边PM的长的最大值为.

查看试题解析
16. 如图，在正方形ABCD中，点E，F分别在边BC，AB上，且 $D E = D F, A C$ 与DE，DF分别交于点M，N.

(1)、若∠ADF=∠EDF，AN= $\sqrt{2}$ 则 $A D =$ ；

(2)、设 $△ D M N$ 和 $△ A F N$ 的面积分别为 $S_{1}$ 和 $S_{2}$ ，若 $S_{2} = 2 S_{1}$ ，则 $\frac{A F}{A D}$ 的值为.

查看试题解析

三、解答题（本大题有8个小题,共72分.解答应写出文字说明、证明过程或演算步骤)

17. 已知 $m = 2 a^{2} b + 3 a b - 4$ .

(1)、当 $a = \frac{1}{b} = 2$ ，求 $m$ 的值.

(2)、当 $b = 202 4^{0}, m = - 4$ 时，求 $a$ 的值.

查看试题解析
18. 如图，在 $△ A B C D$ 中，过点 $A$ 作 $A E ⊥ B C$ 于点 $E, A F ⊥ D C$ 于点 $F$ ，且 $A E = A F$ .

(1)、求证： $▱ A B C D$ 是菱形.

(2)、若 $∠ E A F = 5 6^{°}$ ，求 $∠ D$ 的度数.

查看试题解析

19. 根据以下素材，探索完成“问题解决”中的任务1，任务2和任务3.

背景	2024年4月15日是第9个全民国家安全教育日，为普及国家安全知识，学校开展了“树立防范意识，维护国家安全”的国安知识学习活动.从七、八年级中各随机抽取20名学生进行测试(百分制)，并对数据(成绩)进行整理、描述和分析下面给出了部分信息.
素材1	八年级20名学生测试成绩的频数分布表：
素材2	八年级测试成绩在80<x≤90这一组的数据如下(单位：分)： 81，82，85，86，88，88，89，90
素材3	七、八年级测试成绩的平均数、中位数、众数如表：
问题解决
任务1	求表格中的m= ▲ ， n= ▲ ；
任务2	若小红同学的成绩为84分，在她所属的年级排前10名，根据表中数据判断小红同学是 ▲ 年级的学生（填“七”或“八”)；
任务3	该校八年级共60人参加知识竞赛，估计八年级参加竞赛成绩优秀(x>80)的学生人数.

查看试题解析

20. 中国古代在公元前2世纪就制成了世界上最早的潜望镜，西汉初年成书的《淮南万毕术》中有这样的记载：“取大镜高悬，恳水盆于其下，则见四邻矣”.如图1所示，其工作方法主要利用了光的反射原理.

(1)、在图2中，AB呈水平状态，若入射角 $∠ B C D = 4 1^{°}, ∠ C A E = 3 7^{°}$ (入射角等于反射角，CD，AE为法线)，求∠ABC的度数；

(2)、在(1)的条件下，若AB=11.2米.求点 $C$ 到AB的距离(精确到0.1米).(参考数据： $s i n 3 7^{°} \approx 0.60, c o s 3 7^{°} \approx 0.80, t a n 3 7^{°} \approx 0.75)$

查看试题解析
21. 平面直角坐标系中，反比例函数 $y_{1} = \frac{n}{x} (n \neq 0)$ 与一次函数 $y_{2} = k x + b (k \neq 0)$ 的图象相交于点 $A (1, m), B (- 3, - 1)$ 两点.

(1)、求函数 $y_{1}, y_{2}$ 的表达式；

(2)、将函数 $y_{2}$ 的图象向下平移 $p (p > 0)$ 个单位，新函数的图象与函数 $y_{1} = \frac{n}{x} (x < 0)$ 的图象交于点 $G$ ，如果点 $G$ 的纵坐标是横坐标的3倍，求 $p$ 的值.

查看试题解析
22. 如图，已知AB为 $⊙ O$ 直径，AH相切 $⊙ O$ 于点 $A$ ，点 $C$ 在AB左侧圆弧上，弦 $C D ⊥ A B$ 交 $⊙ O$ 于点 $D$ ，交AB于点 $F$ ，点 $A$ 关于CD的对称点为点 $E$ ，连结EC并延长交AH于点 $G$ ，连结AC，AD.

(1)、求证：∠D=∠CGA；

(2)、当点E在直径AB上时，若 $C E = 5, c o s ∠ C G A = \frac{4}{5}$ ，求 $⊙ O$ 半径的长.

查看试题解析
23. 已知二次函数 $y = a x^{2} + b x - 5 a (a, b$ 是实数， $a \neq 0)$ .

(1)、若该函数图象经过点 $(1, 2), (0, 5)$ ，求该二次函数的表达式及顶点坐标；

(2)、若该函数图象的对称轴为直线 $x = 1, A (x_{1}, y_{1}), B (x_{2}, y_{2})$ 为该函数图象上的任意两点，其中 $x_{1} < x_{2}$ ，求当 $x_{1}, x_{2}$ 为何值时， $y_{1} = y_{2} = 3 a$ ；

(3)、若该二次函数满足当 $x \geq 0$ 时，总有 $y$ 随 $x$ 的增大而减小，且过点 $(1, 3)$ ，当 $a < b$ 时，求 $4 a + b$ 的取值范围.

查看试题解析
24. 定义：两个相似三角形共边且位于一个角的角平分线两边，则称这样的两个相似三角形为叠似三角形.

(1)、【初步理解】
如图1，四边形ABCD中，对角线AC平分 $∠ B A D, ∠ B C D + \frac{1}{2} ∠ B A D = 18 0^{°}$ ，求证： $△ A C B$ 和 $△ A D C$ 为叠似三角形.

(2)、【尝试应用】
在(1)的基础上，如图2，若 $C D / / A B, A D = 4, A C = 6$ ，求四边形ABCD的周长.

(3)、【拓展提高】
如图3，在△ACB中， $D$ 是BC上一点，连接AD，点 $E$ 在AD上，且 $D E = D C, F$ 为AC中点，且 $∠ B E C = ∠ A E F$ .若 $B C = 9, A E = 4$ ，求 $\frac{E F}{B E}$ 的值.

查看试题解析