浙江宁波北仑顾国和外国语2023-2024第二学期八年级下学期数学学生发展过程性评价(5月月考)
试卷更新日期:2024-07-04 类型:月考试卷
一、选择题(每题3分)
-
1. 下列二次根式中,是最简二次根式的是( )A、 B、 C、 D、2. 在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( )A、中位数 B、方差 C、平均数 D、众数3. 用配方法解方程 时,配方结果正确的是( )
A、 B、 C、 D、4. 如图,矩形ABCD中, , 点为直线AB的一点,连EC,平移EC至DF,连接DE、CF,则四边形DECF的面积是( ) A、15 B、40 C、20 D、305. 已知反比例函数的图象位于第一、三象限,则的取值范围是( )A、 B、 C、 D、6. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、15 B、40 C、20 D、305. 已知反比例函数的图象位于第一、三象限,则的取值范围是( )A、 B、 C、 D、6. 用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A、 B、
B、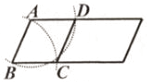 C、
C、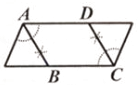 D、
D、 7. 若关于的一元二次方程有实数根,则的取值范围为( )A、 B、且 C、 D、且8. 利用反证法证明“直角三角形至少有一个锐角不小于45°”,应先假设( )A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°9. 已知点是二次函数上的两点,若 , , 则下列关系正确的是( )A、 B、 C、 D、10. 如图,直线交正方形ABCD的对边AD、BC于点P、Q,正方形ABCD和正方形EFGH关于直线成轴对称,点在CD边上,点在边FE上,BC、HG交于点M,AB、FG交于点.以下结论错误的是( )
7. 若关于的一元二次方程有实数根,则的取值范围为( )A、 B、且 C、 D、且8. 利用反证法证明“直角三角形至少有一个锐角不小于45°”,应先假设( )A、直角三角形的每个锐角都小于45° B、直角三角形有一个锐角大于45° C、直角三角形的每个锐角都大于45° D、直角三角形有一个锐角小于45°9. 已知点是二次函数上的两点,若 , , 则下列关系正确的是( )A、 B、 C、 D、10. 如图,直线交正方形ABCD的对边AD、BC于点P、Q,正方形ABCD和正方形EFGH关于直线成轴对称,点在CD边上,点在边FE上,BC、HG交于点M,AB、FG交于点.以下结论错误的是( ) A、 B、的周长等于线段CH的长 C、的周长等于线段CM的长 D、的周长等于
A、 B、的周长等于线段CH的长 C、的周长等于线段CM的长 D、的周长等于二、填空题(每题3分)
-
11. 二次根式 中, x的取值范围是.12. 一个多边形的每一个外角都等于72°,则这个多边形是边形.13. 设 , 则的值是.14. 为执行国家药品降价政策,给人民群众带来实惠,某药品经过两次降价,每盒零售价由50元降为39元,设平均每次降价的百分率是 , 则根据题意,可列方程为.15. 已知二次函数(其中是自变量),当时,随的增大而增大,且时,的最小值为-7,则的值为.16. 如图,在直角坐标系中,直线交坐标轴于A、B两点,函数的图象为曲线.
 (1)、若曲线与直线有唯一的公共点,则;(2)、若曲线使得线段AB上的整点(横纵坐标均为整数的点,且不包括点A、B)分布在它的两侧(上方和下方),每侧的整点个数相同,则k的取值范围为.
(1)、若曲线与直线有唯一的公共点,则;(2)、若曲线使得线段AB上的整点(横纵坐标均为整数的点,且不包括点A、B)分布在它的两侧(上方和下方),每侧的整点个数相同,则k的取值范围为.三、解答题(17~19每题6分,20~22每题8分,23题10分
-
17.(1)、计算:(2)、解方程:18. 如图,反比例函数与一次函数的图象相交于两点.
 (1)、求反比例函数和一次函数的解析式;(2)、设直线AB交轴于点 , 点是轴正半轴上的一个动点,过点作轴交反比例函数的图象于点 , 连CN,OM.若 , 求的取值范围.19. 某班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同条件下,分别对两名同学进行了8次一分钟跳绳测试,现将测试结果绘制成如下统计图表,请根据统计图表中的信息解答下列问题:
(1)、求反比例函数和一次函数的解析式;(2)、设直线AB交轴于点 , 点是轴正半轴上的一个动点,过点作轴交反比例函数的图象于点 , 连CN,OM.若 , 求的取值范围.19. 某班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛,在相同条件下,分别对两名同学进行了8次一分钟跳绳测试,现将测试结果绘制成如下统计图表,请根据统计图表中的信息解答下列问题: (1)、表中;.(2)、求出乙得分的方差.(3)、根据已有的信息,你认为应选谁参赛较好,请说明理由.
(1)、表中;.(2)、求出乙得分的方差.(3)、根据已有的信息,你认为应选谁参赛较好,请说明理由.平均数(分)
中位数(分)
众数(分)
方差(分)
甲
175
93.75
乙
175
175
180
20. 如图1,在平行四边形ABCD中,点E、F分别为AD,BC的中点,点G,H在对角线BD上,且. (1)、求证:四边形EHFG是平行四边形.(2)、如图2,连AC交BD于点 , 若 , 求HF的长.21. 如图1是一架菱形风筝,它的骨架由如图2的4条竹棒AC,BD,EF,GH组成,其中E,F,G,H分别是菱形四边的中点,现有一根长为的竹棒,正好锯成风筝的四条骨架,设菱形的面积为.
(1)、求证:四边形EHFG是平行四边形.(2)、如图2,连AC交BD于点 , 若 , 求HF的长.21. 如图1是一架菱形风筝,它的骨架由如图2的4条竹棒AC,BD,EF,GH组成,其中E,F,G,H分别是菱形四边的中点,现有一根长为的竹棒,正好锯成风筝的四条骨架,设菱形的面积为.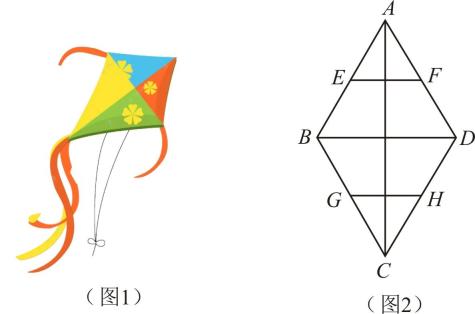 (1)、写出y关于的函数关系式:(2)、为了使风筝在空中有较好的稳定性,要求 , 那么当骨架的长为多少时,这风筝即菱形的面积最大?此时最大面积为多少?22. 如图,在边长为8的正方形ABCD中,点E、G分别在边AB、AD上,且 , 作与GH交于点 , 分别在OF、OH上截取 , 连结PH、QF交于点
(1)、写出y关于的函数关系式:(2)、为了使风筝在空中有较好的稳定性,要求 , 那么当骨架的长为多少时,这风筝即菱形的面积最大?此时最大面积为多少?22. 如图,在边长为8的正方形ABCD中,点E、G分别在边AB、AD上,且 , 作与GH交于点 , 分别在OF、OH上截取 , 连结PH、QF交于点 (1)、四边形EBHO的面积四边形GOFD的面积(填“>”、“=”,或“<”);(2)、比较与大小,并说明理由。(3)、求四边形OQIP的面积.23. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴、轴上,且为直线AC上一动点,连OE,过作 , 交直线BC、直线OA于点F、G,连OF.
(1)、四边形EBHO的面积四边形GOFD的面积(填“>”、“=”,或“<”);(2)、比较与大小,并说明理由。(3)、求四边形OQIP的面积.23. 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴、轴上,且为直线AC上一动点,连OE,过作 , 交直线BC、直线OA于点F、G,连OF. (1)、求直线AC的解析式.(2)、当E为AC中点时,求CF的长.(3)、在点E的运动过程中,坐标平面内是否存在点 , 使得以P、O、G、F为顶点的四边形为菱形,若存在,求出点的横坐标,若不存在,请说明理由.
(1)、求直线AC的解析式.(2)、当E为AC中点时,求CF的长.(3)、在点E的运动过程中,坐标平面内是否存在点 , 使得以P、O、G、F为顶点的四边形为菱形,若存在,求出点的横坐标,若不存在,请说明理由.