新疆维吾尔自治区乌鲁木齐市新市区教育集团2023-2024学年九年级下学期开学数学试题
试卷更新日期:2024-07-04 类型:开学考试
一、选择题(共9小题,每小题4分,共36分.)
-
1. -17的相反数是( )A、-17 B、17 C、 D、2. 下列图形中,为圆柱的侧面展开图的是( )A、
 B、
B、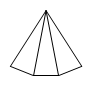 C、
C、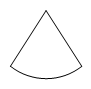 D、
D、 3. 已知点
3. 已知点 与点
与点 关于x轴对称,那么a、b的值为( ) A、 B、 C、 D、4.
关于x轴对称,那么a、b的值为( ) A、 B、 C、 D、4.如图,下列条件中能判定AB∥CD的是( )
 A、∠1=∠2 B、∠2=∠4 C、∠1=∠3 D、∠B+∠BCD=180°5. 下列计算正确的是( )A、x2+x3=x5B、x2•x4=x8 C、x6÷x2=x3 D、(x2)3=x66. 若一元二次方程x2+2x+m=0有实数解,则m的取值范围是( )A、m≤-1 B、m≤1 C、m≤1 D、m≤47. 抛物线
A、∠1=∠2 B、∠2=∠4 C、∠1=∠3 D、∠B+∠BCD=180°5. 下列计算正确的是( )A、x2+x3=x5B、x2•x4=x8 C、x6÷x2=x3 D、(x2)3=x66. 若一元二次方程x2+2x+m=0有实数解,则m的取值范围是( )A、m≤-1 B、m≤1 C、m≤1 D、m≤47. 抛物线 的最低点的坐标是( ) A、 B、 C、(3. -5) D、8. 为迎接中秋佳节的到来,时代超市某品牌的月饼零售价经过两次降价后的价格为降价前的81%,则平均每次降价( )A、19% B、9.5% C、10% D、20%9. 下列图形都是有几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,按此规律,图⑩中黑色正方形的个数是( )
的最低点的坐标是( ) A、 B、 C、(3. -5) D、8. 为迎接中秋佳节的到来,时代超市某品牌的月饼零售价经过两次降价后的价格为降价前的81%,则平均每次降价( )A、19% B、9.5% C、10% D、20%9. 下列图形都是有几个黑色和白色的正方形按一定规律组成,图①中有2个黑色正方形,图②中有5个黑色正方形,图③中有8个黑色正方形,图④中有11个黑色正方形,…,按此规律,图⑩中黑色正方形的个数是( ) A、32 B、29 C、28 D、26
A、32 B、29 C、28 D、26二、填空题(共6小题,每小题4分,共24分.)
-
10. 式子在实数范围内有意义,则x的取值范围是 .11. 若反比例函数 的图象经过点 , 则k的值是.12. 如图是一个游戏转盘,连续自由转动转盘两次(如果落在分隔线上,则重新转动,直至转到其中一块区域),则两次转动指针都落在数字“蓝色”所示区域内的概率是 .
 13. 已知 中, 直径 , 弦 A C 的长为 3cm, 则弦 A C的长为3cm,则弦AC所对圆周角的度数为 .14. 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论正确的是 :
13. 已知 中, 直径 , 弦 A C 的长为 3cm, 则弦 A C的长为3cm,则弦AC所对圆周角的度数为 .14. 从地面竖直向上抛出一小球,小球的高度h(单位:m)与小球运动时间t(单位:s)之间的函数关系如图所示.下列结论正确的是 :①小球在空中经过的路程是40m;
②小球抛出3秒后,速度越来越快;
③小球抛出3秒时,速度为0m/s;
④小球的高度h=30m时,t=1.5s.
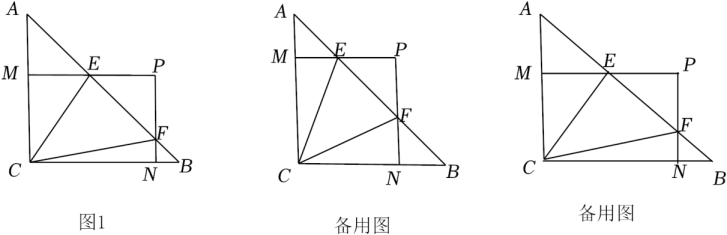
 15. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:
15. 如图,已知正方形ABCD,点M是边BA延长线上的动点(不与点A重合),且AM<AB,△CBE由平移得到,若过点E作EH⊥AC,H为垂足,则有以下结论:①点M位置变化,使得∠DHC=60°时,2BE=DM;
②无论点M运动到何处,都有DM=HM;
③在点M的运动过程中,四边形CEMD不可能成为菱形;
④无论点M运动到何处,∠CHM一定大于135°.
以上结论正确的有(把所有正确结论的序号都填上).

三、解答题(共8小题,共90分.)
-
16. 计算(1)、(2)、17.(1)、解不等式组:(2)、某超市销售A、B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.求:A、B两款保温杯的销售单价各是多少元?18. 如图,点E , F在BC上,BE=CF, 与 D E 交于点O .
 (1)、求证:;(2)、若 , 求 的度数19. 垃圾的分类回收不仅能够减少环境污染、美化家园,甚至能够变废为宝、节约资源.为增强学生垃圾分类意识,推动垃圾分类进校园,赤峰市某中学组织全校1565名学生参加了“垃圾分类知识竞赛”(满分为100分).该校数学兴趣小组为了解全校学生竞赛分数情况,采用简单随机抽样的方法(即每名学生的竞赛分数被抽到的可能性相等的抽样方法)抽取部分学生的竞赛分数进行调查分析.(1)、以下三种抽样调查方案中,抽取的样本最具有代表性和广泛性的一种抽样调查方案是(填“方案一”“方案二”或“方案三”)
(1)、求证:;(2)、若 , 求 的度数19. 垃圾的分类回收不仅能够减少环境污染、美化家园,甚至能够变废为宝、节约资源.为增强学生垃圾分类意识,推动垃圾分类进校园,赤峰市某中学组织全校1565名学生参加了“垃圾分类知识竞赛”(满分为100分).该校数学兴趣小组为了解全校学生竞赛分数情况,采用简单随机抽样的方法(即每名学生的竞赛分数被抽到的可能性相等的抽样方法)抽取部分学生的竞赛分数进行调查分析.(1)、以下三种抽样调查方案中,抽取的样本最具有代表性和广泛性的一种抽样调查方案是(填“方案一”“方案二”或“方案三”)方案一:从七年级、八年级、九年级中指定部分学生的竞赛分数作为样本;
方案二:从七年级、八年级中随机抽取部分男生的竞赛分数以及在九年级中随机抽取部分女生的竞赛分数作为样本;
方案三:从全校1565名学生的竞赛分数中随机抽取部分学生的竞赛分数作为样本.
(2)、该校数学兴趣小组根据简单随机抽样方法获得的样本,绘制出如下统计表(90分及以上为“优秀”,60分及以上为“及格”,学生竞赛分数记为x分)分数段
50≤x<60
60≤x<70
8
50≤x<90
90≤x≤100
频数
5
7
18
30
40
结合上述信息解答下列问题:
①样本数据的中位数所在分数段为 ▲ ;
②估计全校学生中竞赛分数达到“优秀”的学生有多少人.
(3)、样本数据中,九(1)班的竞赛分数为“优秀”的学生有4人,其中3名男生、1名女生,现要从这4名学生中随机抽取2人给全校学生进行垃圾分类知识宣讲,请用画树状图或列表的方法,求抽到的2名学生为一男一女的概率.20. 某合作社为尽快打开市场,对芸豆进行线上和线下销售相结合的模式,具体销售模式如下:线下销售模式,标价5元/千克,八折出售;
线上销售模式:标价5元/千克,九折出售,超过6千克的,超出部分每千克再让利1.5元.
设购买威宁芸豆x千克,所需费用为y元,y与x之间的函数关系如图所示.
根据以上信息,解决下列问题:
 (1)、求两种销售模式分别对应的函数表达式;(2)、求出图中点C的坐标,并说明其实际意义;(3)、若想购买10千克威宁芸豆,请问选择哪种模式购买更省钱?21. 某乡镇为创建特色小镇,助力乡村振兴,决定在某山旁的一条河上修建一座步行观光桥,因此要先测量河宽CD.如图,在河岸C处测得山顶B的仰角为45°,在对岸D处测得山顶B的仰角为33 °.已知山高,BA-100m点A与河岸C,D在同一水平线上,求河宽CD(结果精确到1m.参考数据:).
(1)、求两种销售模式分别对应的函数表达式;(2)、求出图中点C的坐标,并说明其实际意义;(3)、若想购买10千克威宁芸豆,请问选择哪种模式购买更省钱?21. 某乡镇为创建特色小镇,助力乡村振兴,决定在某山旁的一条河上修建一座步行观光桥,因此要先测量河宽CD.如图,在河岸C处测得山顶B的仰角为45°,在对岸D处测得山顶B的仰角为33 °.已知山高,BA-100m点A与河岸C,D在同一水平线上,求河宽CD(结果精确到1m.参考数据:).