新人教版（2024版）七年级上学期数学第四章质量检测

试卷更新日期：2024-07-04 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 已知 $a^{2} + b c = 3$ ， $b^{2} - 2 b c = - 2$ ．则 $5 a^{2} + 4 b^{2} - 3 b c$ 的值是（）

A、 $- 23$ B、7 C、13 D、23

查看试题解析
2. 已知M＝2x²+x﹣6，N＝x²﹣x﹣7，则M、N的大小关系是（　　）

A、M＝N B、M≥N C、M≤N D、不能确定

查看试题解析
3. 如图，大长方形ABCD是由正方形一、二、三、五和小长方形四拼成的，且正方形一、二、三的边长分别为a ， b ， c（ $a < b < c$ ），有以下结论：① $a + b > c$ ；②小长方形四的宽是 $b + c - a$ ；③ $a + c = 2 b$ ；④大长方形ABCD的周长为 $2 a + 2 b + 2 c ．$ 其中正确的结论有（）

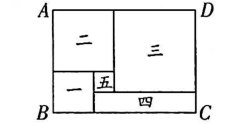A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共15分）

三、计算题（共12分）

4. 合并下列各式的同类项：

(1)、 $3 a + 2 b - 5 a - b$

(2)、 $x + (5 x - 3 y) - (x - 2 y)$

(3)、 $(2 m^{2} n - 5 m n) - 2 (- m n - m^{2} n)$

(4)、 $(- p^{2} + 3 p q - \frac{1}{2} q^{2}) - (- \frac{1}{2} p^{2} + 4 p q - \frac{3}{2} q^{2})$

查看试题解析

四、解答题（共7题，共63分）

5. A、B、C．D四个车站的位置如图所示，车站B距车站A、D的距离分别为 $(a + b) k m$ 、 $(5 a + 36) k m$ ，车站C与车站D的距离为 $(3 a + 2 b) k m$ ．其中a，b是不为0的实数．

(1)、求B、C两站之间的距离（用含a、b的代数式表示）．

(2)、若B、D两个车站之间的距离比A、B两个车站之间的距离长8km，求出B、C两个车站相距多少km？

查看试题解析
6. 已知代数式 $A = 2 x^{2} + 5 x y - 7 y - 3$ ， $B = x^{2} - x y + 2$

(1)、求 $3 A - (2 A + 3 B)$ 的值；

(2)、若 $A - 2 B$ 值与 $x$ 的取值无关，求 $y$ 的值．

查看试题解析
7. 绿源超市销售茶壶、茶杯，茶壶每只定价50元，茶杯每只定价6元．春节期间，超市将开展促销活动，向顾客提供两种优惠方案：
方案一：每买一只茶壶就赠一只茶杯；
方案二：茶壶和茶杯都按定价的90%付款．
某顾客计划到该超市购买茶壶8只和茶杯x只（茶杯数多于8只）．

(1)、用含x的代数式分别表示方案一与方案二各需付款多少元？

(2)、当 $x = 15$ 时，请通过计算说明该顾客选择上面的两种购买方案哪种更省钱？

查看试题解析
8. 有理数a ， b ， c在数轴上的位置如图所示．

(1)、由图可得：a－c0，a－b0，b－c0（填＜，＞，＝）；

(2)、结合（1）化简： $| a - c | + | a - b | - | b - c |$ ．

查看试题解析
9. 初一某班小明同学做一道数学题，“已知两个多项式 $A = □ x^{2} - 4 x$ ， $B = 2 x^{2} + 3 x - 4$ ，试求 $A + 2 B$ ． ”其中多项式A的二次项系数印刷不清楚．

(1)、小明看答案以后知道 $A + 2 B = x^{2} + 2 x - 8$ ，则印刷不清楚的系数是；

(2)、在（1）的基础上，小明已经将多项式A正确求出，老师又给出了一个多项式 $C = - 7 x^{2} - 8 x + 2$ ，要求小明求出 $A - C$ 的结果，请你替小明求出“ $A - C$ ”的正确答案．

查看试题解析
10. 数轴上有三个点A，B，C，分别代表的整数是a，b，c，点C在数轴上的位置如图，a，b满足|a+8|+(b-2)²=0．

(1)、a= ， c= ，点A与点B之间的距离是

(2)、点A以每秒2个单位长度的速度向左运动，点B以每秒4个单位长度的速度向左运动，点C以每秒a个单位长度的速度向右运动，点A，B，C同时运动，设运动时间为t秒，回答下列问题：
①t秒时，点A对应的数为 ▲ (用含t的式子表示)；
②当t>5时，点A与点B之间的距离是 ▲ (用含t的式子表示)；
③若点A与点C之间的距离记为d₁ ，点B与点C之间的距离记为d₂ ，是否存在有理数a，使得代数式3d₁-2d₂的值为定值？若存在，求出a的值及该定值，若不存在，请说明理由．

查看试题解析
11. 近年来，电商多选择在11月11日促销．今年的促销期间，某电商客服在为买家包装商品时用到长、宽、高分别为a厘米、b厘米、c厘米的箱子，并发现有如图所示的乙两种打包方式（打包带不计接头处的长）．回答下列问题：

(1)、用含a，b， c的式子表示甲、乙两种打包方式所用的打包带的长度：
甲需要厘米，乙需要厘米；

(2)、当a=50厘米，b=40厘米，c=30厘米时，直接写出甲、乙两种打包方式所用的打包带的长度：甲需要厘米，乙需要厘米；

(3)、当a>b>c时，两种打包方式中，哪种方式节省打包带？并说明你的理由．

查看试题解析