【培优版】北师大版数学九上第一章特殊的平行四边形单元测试卷

试卷更新日期：2024-07-03 类型：单元试卷

进入出卷网下载

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

1. 如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（　　）

A、2 $\sqrt{3}$ +2 B、5- $\frac{\sqrt{3}}{3}$ C、3- $\sqrt{3}$ D、 $\sqrt{3}$ +1

查看试题解析
2. 如图，在正方形ABCD外取一点E ，连接AE ， BE ， DE ．过点A作AE的垂线交DE于点P $A E = A P = 1$ ， $P B = \sqrt{5}$ ．下列结论：① $△ A P D ≌ △ A E B$ ；② $E B ⊥ E D$ ；③点B到直线AE的距离是 $\frac{\sqrt{6}}{3}$ ；④ $S_{正方形 A B C D} 4 + \sqrt{6}$ ．其中所有正确的结论是（）

A、② ③ B、① ④ C、① ② ④ D、① ② ③ ④

查看试题解析
3. 如图，四边形 $A B C D$ 中， $A B = B C ， ∠ A B C = 90 °$ ，点 $O$ 为对角线 $A C$ 的中点， $B E ⊥ C D$ 于点 $E$ ，若 $∠ D B E = 45 °$ ， $∠ C O E = α$ ，则 $∠ C A D$ 的度数是（）

A、 $45 ° + α$ B、 $90 ° - α$ C、 $3 α$ D、 $135 ° - 3 α$

查看试题解析
4. 如图，在正方形 $A B C D$ 中，点 $E$ ， $F$ 分别在 $B C$ ， $C D$ 上，连接 $A E$ ， $A F$ ， $E F$ ， $∠ E A F = 45 °$ ．若 $∠ B A E = α$ ，则 $∠ F E C$ 一定等于（）

A、 $2 α$ B、 $90 ° - 2 α$ C、 $45 ° - α$ D、 $90 ° - α$

查看试题解析
5. 如图，在菱形ABCD中，∠BAD=60°，AC与BD交于点O，E为CD延长线上的一点，且CD=DE，连接BE分别交AC、AD于点F、G，连接OG，则下列结论：①OG= $\frac{1}{2}$ AB②与△DEG全等的三角形共有5个：③四边形ODEG与四边形OBAG面积相等：④由点A、B、D、E构成的四边形是菱形。其中一定成立的是（）

A、①③④ B、①②③ C、①②④ D、②③④

查看试题解析
6. 已知菱形OABC在平面直角坐标系的位置如图所示，顶点 $A (5 ， 0)$ ， $B (8 ， 4)$ ，点P是对角线OB上的一个动点， $D (0 ， 1)$ ，当 $C P + D P$ 最短时，点P的坐标为（）

A、 $(0 ， 0)$ B、 $(1 ， \frac{1}{2})$ C、 $(\frac{6}{5} ， \frac{3}{5})$ D、 $(\frac{10}{7} ， \frac{5}{7})$

查看试题解析
7. 如图，在平面直角坐标系中，菱形 $O A B C$ 的边长为 $2 \sqrt{6}$ ，点 $B$ 在 $x$ 轴的正半轴上，且 $∠ A O C = 60 °$ ，将菱形 $O A B C$ 绕原点 $O$ 逆时针方向旋转 $60 °$ ，得到四边形 $O A' B' C' ($ 点 $A'$ 与点 $C$ 重合 $)$ ，则点 $B'$ 的坐标是（）

A、 $(3 \sqrt{6} ， 3 \sqrt{2})$ B、 $(3 \sqrt{2} ， 3 \sqrt{6})$ C、 $(3 \sqrt{2} ， 6 \sqrt{2})$ D、 $(6 \sqrt{2} ， 3 \sqrt{6})$

查看试题解析

二、填空题（本大题共5小题, 每小题3分, 共15分)

8. 如图，菱形ABCD中，∠ABC＝60°，AB＝2，E、F分别是边BC和对角线BD上的动点，且BE＝DF ，则AE+AF的最小值为．

查看试题解析
9. 如图，四边形ABCD是正方形，点 $E$ 是线段BC上的动点，以BE为边作正方形BEFG，连接AF，M为AF的中点，且 $A B = 4$ ，则线段EM的最小值是.

查看试题解析
10. 如图，在矩形纸片ABCD中，AB＝7，AD＝6 $\sqrt{5}$ ，点E是AD边上一动点，连接BE．将△ABE沿BE折叠得到△FBE，连接FC．当△BCF的面积为6 $\sqrt{5}$ 时，线段AE的长为．

查看试题解析
11. 四边形ABCD是正方形，点E是直线AD上的一点，连接CE（C、E、F、G四个点按照逆时针方向排序），直线BE与直线GD交于点H ，若AE＝2，则点F到GH的距离为．

查看试题解析
12. 如图，在边长为10的菱形 $A B C D$ 中，对角线 $B D = 16$ ，点O是线段 $B D$ 上的动点， $O E ⊥ A B$ 于E， $O F ⊥ A D$ 于F.则 $O E + O F =$ .

查看试题解析

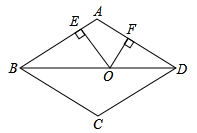
三、解答题

13. 在正方形ABCD中，点E为对角线AC（不含点A）上的任意一点，AB= $2 \sqrt{2}$ ，

(1)、如图1，将△ADE绕点D逆时针旋转90°得到△DCF，连接EF
①把图形补充完整（无需写画法），②求EF²的取值范围；

(2)、如图2，求BE+AE+DE的最小值

查看试题解析
14. 如图，在正方形 $A B C D$ 中，点 $E$ 是对角线 $A C$ 上一动点，连接 $D E$ ，作 $E F ⊥ D E$ 交 $B C$ 于点 $F$ ，以 $E D$ 和 $E F$ 为邻边作矩形 $E F G D$ ．

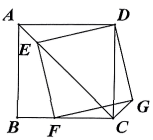(1)、猜想： $A E$ ， $C G$ 的位置关系是；

(2)、求证： $△ D A E ≌ △ D C G$ ．

查看试题解析
15. 如图，在正方形ABCD中，AB＝4，点E是对角线AC上的一点，连接DE，过点E作EF⊥DE，交AB于点F，以DE，EF为邻边作矩形GFED，连接AG，

(1)、求证：矩形GFED是正方形。

(2)、求AG+AE的值。

查看试题解析
16. 如图1，在正方形 $A B C D$ 中， $E$ 是 $A B$ 上一点， $F$ 是 $A D$ 延长线上一点，且 $D F = B E$ .

(1)、求证： $C E = C F$ ；

(2)、在图1中，若 $G$ 在 $A D$ 上，且 $∠ G C E = 45 °$ ，则 $G E = B E + G D$ 成立吗？为什么？

(3)、运用（1）（2）解答中所积累的经验和知识，完成下题：
①如图2，在直角梯形 $A B C D$ 中， $A D ∥ B C (B C > A D)$ ， $∠ B = 90 °$ ， $A B = B C = 12$ ， $E$ 是 $A B$ 上一点，且 $∠ D C E = 45 °$ ， $B E = 4$ ，则 $D E$ 的长为（直接写出结果，不需要写出计算过程）.
②如图3，在 $△ A B C$ 中， $∠ B A C = 45 °$ ， $A D ⊥ B C$ ， $B D = 2$ ， $C D = 3$ ，则 $△ A B C$ 的面积为（直接写出结果，不需要写出计算过程）

查看试题解析
17. 已知：如图，在矩形 $A B C D$ 中，点 $E$ 在边 $B C$ 上，以 $D E$ 为边作矩形 $D E G F$ ，其中 $G F$ 经过点 $A$ ，连接 $A E$ 、 $B G$ ．
　　

(1)、若点 $A$ 是 $G F$ 的中点，求证： $E D$ 是 $∠ A E C$ 的平分线；

(2)、若 $B G = A G$ ， $C E = 1$ ， $A F = 2$ ，求 $A D$ 的长；

(3)、若四边形 $A B C D$ 是边长为 $10$ 的正方形， $B G = B E$ ，求出 $A G$ 的长．

查看试题解析
18. 实践操作：第一步：如图1，将矩形纸片 $A B C D$ 沿过点D的直线折叠，使点A落在 $C D$ 上的点 $A^{'}$ 处，得到折痕 $D E$ ，然后把纸片展平．第二步：如图2，将图1中的矩形纸片 $A B C D$ 沿过点E的直线折叠，点C恰好落在 $A D$ 上的点 $C^{'}$ 处，点B落在点 $B^{'}$ 处，得到折痕 $E F$ ， $B^{'} C^{'}$ 交 $A B$ 于点M， $C^{'} F$ 交 $D E$ 于点N，再把纸片展平．

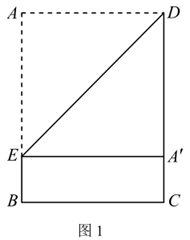
问题解决：

(1)、如图1，填空：四边形 $A E A^{'} D$ 的形状是；

(2)、如图2，线段 $M C^{'}$ 与 $M E$ 是否相等？若相等，请给出证明；若不等，请说明理由；

(3)、如图2，若 $A C^{'} = 2 cm ， D C' = 4 cm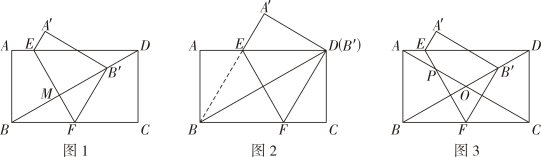$ ，求 $D N ： E N$ 的值．

查看试题解析
19. 综合与实践
[问题情境]
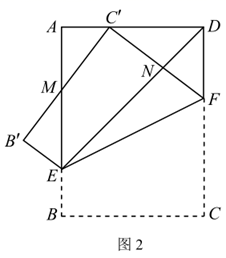
如图1，小华将矩形纸片ABCD先沿对角线BD折叠，展开后再折叠，使点B落在对角线BD上，点B的对应点记为B'，折痕与边AD，BC分别交于点E，F．

(1)、 [活动猜想]如图2，当点B'与点D重合时，四边形BEDF是哪种特殊的四边形？并给予证明．

(2)、 [问题解决]如图1，当AB=4， AD=8，BF=3时，连结B'C，则B'C的长为

(3)、 [深入探究]如图3，请直接写出AB与BC满足什么关系时，始终有A'B'与对角线AC平行？

查看试题解析

【培优版】北师大版数学九上第一章 特殊的平行四边形 单元测试卷

一、选择题(本大题共 8 小题, 每小题 3 分, 共 24 分, 每小题有四个选项, 其中只有一个是正确的）

二、填空题（本大题共5小题, 每小题3分, 共15分)

三、解答题

【培优版】北师大版数学九上第一章特殊的平行四边形单元测试卷