人教版九年级上学期数学第二十二章质量检测

试卷更新日期：2024-07-03 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 一次函数 $y = a x + b$ 与二次函数 $y = a x^{2} + b x$ 在同一坐标系中的图象大致为（）

A、 B、 C、 D、

查看试题解析
2. 抛物线 $y = - 2 x^{2} + 1$ 通过变换可以得到抛物线 $y = - 2 {(x + 1)}^{2} + 3$ ，以下变换过程正确的是（）

A、先向右平移1个单位，再向上平移2个单位 B、先向左平移1个单位，再向下平移2个单位 C、先向右平移1个单位，再向下平移2个单位 D、先向左平移1个单位，再向上平移2个单位

查看试题解析
3. 下列各式中，y是x的二次函数的是（）

A、 $y = \frac{1}{x^{2}}$ B、 $y = x^{2} + \frac{1}{x} + 1$ C、 $y = 2 x^{2} - 1$ D、 $y = \sqrt{x^{2} - 1}$

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ 满足以下三个条件：① $\frac{b^{2}}{a} > 4 c$ ， ② $a - b + c < 0$ ， ③ $b < c$ ，则它的图象可能是（）

A、 B、 C、 D、

查看试题解析
5. 已知二次函数 $y = m x^{2} - 4 m x - 5 m + 1 (m < 0)$ 下列结论正确的是（）
①已知点 $M (4, y_{1})$ ，点 $N (- 2, y_{2})$ 在二次函数的图象上，则 $y_{1} > y_{2}$ ；②该图象一定过定点 $(5, 1)$ 和 $(- 1, 1)$ ；③直线 $y = x - 1$ 与抛物线 $y = m x^{2} - 4 m x - 5 m + 1$ 一定存在两个交点；④当 $- 3 \leq x \leq 1$ 时， $y$ 的最小值是 $m$ ，则 $m = \frac{1}{9}$ ．

A、①②③ B、①③④ C、②③④ D、①②③④

查看试题解析
6. 已知二次函数 $y = x^{2} - b x + 1$ ，当 $- \frac{3}{2} \leq x \leq \frac{1}{2}$ 时，函数 $y$ 有最小值 $\frac{1}{2}$ ，则b的值为（）

A、 $- \sqrt{2}$ 或 $\frac{3}{2}$ B、 $- \frac{11}{6}$ 或 $\frac{3}{2}$ C、 $\pm \sqrt{2}$ D、 $- \sqrt{2}$ 或 $- \frac{11}{6}$

查看试题解析
7. 已知二次函数 $y = x^{2} - 5 x + m$ （m为常数）的图象与x轴的一个交点为 $(1 ， 0)$ ，则关于x的一元二次方程 $x^{2} - 5 x + m = 0$ 的两个实数根是（）

A、 $x_{1} = 1$ ， $x_{2} = - 1$ B、 $x_{1} = 1$ ， $x_{2} = 0$ C、 $x_{1} = 1$ ， $x_{2} = 2$ D、 $x_{1} = 1$ ， $x_{2} = 4$

查看试题解析
8. 如图，已知抛物线 $y = a x^{2} + b x + c$ 与直线 $y = k x + m$ 交于 $A (- 3 ， - 1)$ ， $B (0 ， 3)$ 两点，则关于x的不等式 $a x + b x + c > k x + m$ 的解集是（）

A、 $x < - 3$ 或 $x > 0$ B、 $x \leq - 3$ 或 $x \geq 0$ C、 $- 3 < x < 0$ D、 $- 3 \leq x \leq 0$

查看试题解析
9. 在平面直角坐标系中，对于二次函数 $y = x^{2} - 4 x + 5$ ，下列说法中错误的是（）

A、y的最小值为1 B、图象顶点坐标为（2，1），对称轴为直线x=2 C、当 $x < 2$ 时，y的值随x值的增大而增大，当 $x > 2$ 时，y的值随x值的增大而减小 D、它的图象可由 $y = x^{2}$ 的图象向右平移2个单位长度，再向上平移1个单位长度得到

查看试题解析
10. 已知抛物线 $y = - x^{2} + 2 m x + m - 5$ 与 $x$ 轴的两个交点在 $(1 ， 0)$ 两旁，则关于 $x$ 的方程 $\frac{1}{4} x^{2} + (m + 1) x + m^{2} + 5 = 0$ 的根的情况是（）

A、有两个正数根 B、有两个负数根 C、有一个正根和一个负根 D、无实数根

查看试题解析

二、填空题（每题3分，共15分）

11. 若 $y = (m^{2} + m) x^{m^{2} + 1} - x + 3$ 是关于x的二次函数，则m= ．

查看试题解析
12. 如图，在平面直角坐标系中，点 $A (2 ， 4)$ 在抛物线 $y = a x^{2}$ 上，过点A作y轴的垂线，交抛物线于另一点B，点C、D在线段AB上，分别过点C、D作x轴的垂线交抛物线于E、F两点.当四边形CDFE为正方形时，线段CD的长为.

查看试题解析
13. 抛物线y=x²﹣2x+3的顶点坐标是

查看试题解析

三、解答题（共7题，共63分）

14. 为抢抓大数据产业发展先机，紧跟电商发展新机遇、新模式、新业态，贵州省大力打造地方特色电商平台，通过“云”销售，助力“黔货出山”．贵州特产某品牌维C刺梨汁的进价为45元/箱，售价为60元/箱，某销售网店平均每周可售出100箱；而当销售价每降低1元时，平均每周多售出20箱．设每箱产品降价x元，每个周的销售利润为y元

(1)、求y与x的关系式；

(2)、当销售价为多少元时，每周获得的利润最大？并求出最大利润．

查看试题解析
15. 在平面直角坐标系中，已知点A（2m+1，7）在抛物线y＝x²﹣（m+2）x+m（m是常数）上．

(1)、求该二次函数的解析式；

(2)、当m＞0时，若抛物线y＝x²﹣（m+2）x+m与直线y＝x+n（n是常数）在第四象限内有两个交点，请求出n的取值范围．

查看试题解析
16. 在平面直角坐标系xOy中，有抛物线 $y = a x^{2} + b x + 3 (a \neq 0)$ .

(1)、若点 $(2 ， 3)$ 在抛物线上，
①求抛物线的对称轴；
②若点 $(x_{1} ， 6) ， (x_{2} ， - 3)$ 也在抛物线上，求 $a$ 的取值范围；

(2)、当 $a = - 1$ 时，有已知点 $A (b ， 2) ， B (- b ， 4 b - 3)$ ，若抛物线与线段AB只有一个公共点，结合函数图象，求 $b$ 的取值范围.

查看试题解析
17. 如图，直线y $＝ - \frac{2}{3}$ x＋4与x轴交于点C，与y轴交于点B，
抛物线y＝ax² $＋ \frac{10}{3}$ x＋c经过B、C两点．

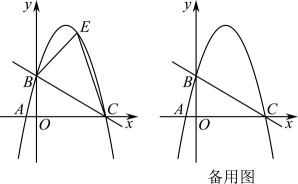(1)、求抛物线的解析式；

(2)、如图，点E是直线BC上方抛物线上的一动点，当△BEC面积最大时，请求出点E的坐标；

查看试题解析
18. 如图1，抛物线 $y = x^{2} + b x + c （ a > 0$ ）与y轴交于点C，与x轴交于A，B两点，点A在点B左侧．点B的坐标为 $(1 ， 0)$ ， $O C = 3 O B$ ．

(1)、求抛物线的解析式；

(2)、若点M是抛物线上的动点，当A、C两点到直线 $B M$ 的距离相等时，求直线 $B M$ 的解析式；

(3)、已知点D、F在抛物线上，点D的横坐标为m $(- 3 < m < - 1)$ ，点F的横坐标为 $m + 1$ ．过点D作x轴的垂线交直线 $A C$ 于点M，过点F作x轴的垂线交直线 $A C$ 于点N．
①如图2，连接 $D F$ ，求四边形 $D F N M$ 的最大值及此时点D的坐标；
②如图3连接 $A D$ 和 $F C$ ，试探究 $△ A D M$ 与 $△ C F N$ 的面积之和是否为定值吗？若是，请求出来；若不是，请说明理由．

查看试题解析
19. 某市政府大力扶持大学生创业，小明在政府的扶持下投资销售一种进价为每千克6元的农产品.销售过程中发现，每天的销售量 $y$ （千克）与销售单价 $x$ （元）之间满足一次函数关系，部分数据如下表所示，另外在销售过程中小明每天需要支付其他费用200元.
销售单价 $x$ （元/千克）
10
11
销售量 $y$ （千克）
300
270

(1)、求 $y$ 与 $x$ 的函数关系式：

(2)、根据物价部门的规定，这种农产品的销售单价不得高于12元，那么如何定价才能使小明每天获得的纯利润最大？最大纯利润是多少元？

查看试题解析

四、实践探究题（共12分）

20. 根据以下材料，探索完成任务：

智能浇灌系统使用方案
材料			如图1是一款智能浇灌系统，水管OP垂直于地面并可以随意调节高度（OP最大高度不超过2.4m），浇灌花木时，喷头P处会向四周喷射水流形成固定形状的抛物线，水流落地点M与点O的距离即为最大浇灌距离，各方向水流落地点形成一个以点O为圆心，OM为半径的圆形浇灌区域．当喷头P位于地面与点O重合时，某一方向的水流上边缘形成了如图2的抛物线，经测量， $O M = 2 m$ ，水流最高时距离地面0.1m．如图3，农科院将该智能浇灌系统应用于一个长8m，宽6m的矩形试验田中，水管放置在矩形中心O处．
问题解决
任务1	确定水流形状	在图2中建立合适的平面直角坐标系，求抛物线的函数表达式．
任务2	探究浇灌最大区域	当调节水管OP的高度时，浇灌的圆形区域面积会发生变化，请你求出最大浇灌圆形区域面积．（结果保留 $π$ ）
任务3	解决具体问题	若要保证浇灌区域能完全覆盖矩形试验田，则水管OP至少需要调节到什么高度？

查看试题解析

销售单价 $x$ （元/千克）	10	11
销售量 $y$ （千克）	300	270