人教版八年级上学期数学第十一章质量检测

试卷更新日期：2024-07-03 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 在△ABC中，作出AC边上的高，正确的是（）.

A、 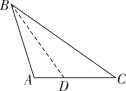B、 C、 D、

查看试题解析
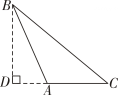2. 已知△ABC的三边长为a，b，c，化简|a＋b－c|－|b－a－c|的结果是（）

A、2b－2c B、－2b C、2a＋2b D、2a

查看试题解析
3. 如图，在五边形ABCDE中，若去掉一个30°的角后得到一个六边形BCDEMN，则∠l+∠2的度数为（　　　）

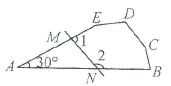A、210° B、110° C、150° D、100°

查看试题解析
4. 将一副三角板按如图所示的方式放置，图中∠CAF的大小等于（）

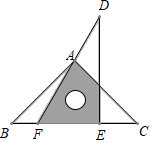A、50° B、60° C、75° D、85°

查看试题解析
5. 如图，△ $A B C$ 为直角三角形， $∠ A C B = 90 °$ ， AD为∠CAB的平分线，与∠ABC的平分线BE交于点E ， BG是△ABC的外角平分线，AD与BG相交于点G ，则∠ADC与∠GBF的和为（）

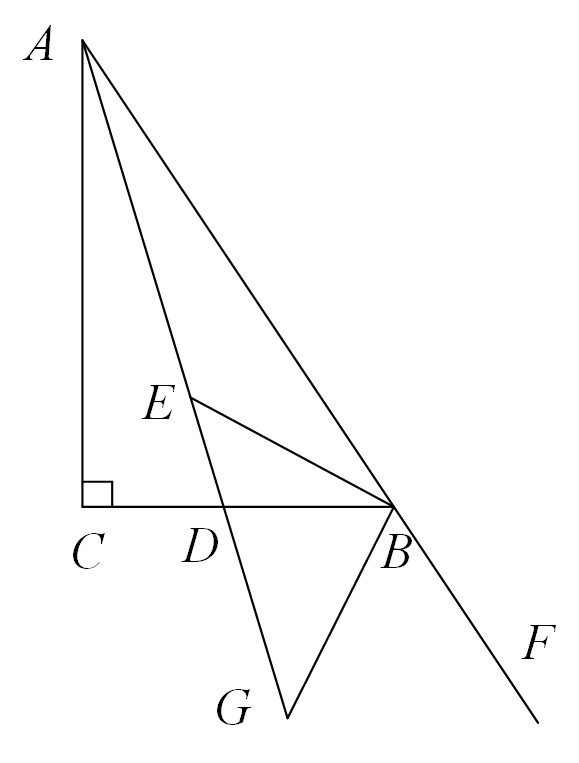A、120° B、135° C、150° D、160°

查看试题解析
6. 如图，南宁白沙大桥是一座斜拉索桥，造型美观，结构稳固，其蕴含的数学道理是（）

A、三角形的稳定性 B、四边形的不稳定性 C、三角形两边之和大于第三边 D、三角形内角和等于 $180 °$

查看试题解析
7. 如图，△ABC的三边的中线AD，BE，CF的公共点为G，且AG：GD=2：1，若S_△_ABC=12，则图中阴影部分的面积是（）

A、3 B、4 C、5 D、6

查看试题解析
8. 如图， $∠ A B C = ∠ A C B$ ， $B D$ 、 $C D$ 、 $A D$ 分别平分 $∠ A B C$ 、 $∠ A C F$ 、 $∠ E A C$ ．以下结论，其中正确的是（）
① $A D ∥ B C$ ；② $∠ A D B = \frac{1}{2} ∠ A C B$ ；③ $∠ B A C = 2 ∠ B D C$ ；④ $∠ A D C + ∠ A B D = 90 °$ ．

A、①② B、②③④ C、①③④ D、①②③④

查看试题解析

二、填空题（每题3分，共15分）

9. 过某个多边形一个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是边形．

查看试题解析

三、解答题（共7题，共65分）

10. 如图， $D$ ， $E$ ， $F$ ， $G$ 分别是 $△ A B C$ 边上的点， $∠ 1 + ∠ 2 = 180 °$ ， $∠ B = ∠ 3$ ．

(1)、求证： $D E ∥ B C$ ；

(2)、若 $∠ C = 76 °$ ， $∠ A E D = 2 ∠ B$ ，请直接写出 $∠ A E F$ 的度数．

查看试题解析
11. 若一个多边形的内角和的 $\frac{1}{4}$ 比它的外角和多 $90 °$ ，那么这个多边形的边数是多少？

查看试题解析
12. 如图，在 $△ A B C$ 中， $A D$ 是高，角平分线 $A E ， B F$ 相交于点 $O$ ， $∠ B A C = 5 0^{∘}$ ， $∠ C = 7 0^{∘}$ ，求 $∠ C A D$ 和 $∠ A O B$ 的度数．

查看试题解析
13. 中华人民共和国五星红旗上大五角星代表中国共产党，四颗小五角星代表工人、农民、小资产阶级和民族资产阶级四个阶级．五颗五角星互相连缀、疏密相间，象征中国人民大团结．每颗小星各有一个尖角正对大星中心点，表示人民对党的向心之意，如图①：根据图形填空：

(1)、 $∠ 1 = ∠ C +$ ， $∠ 2 = ∠ B +$ ；

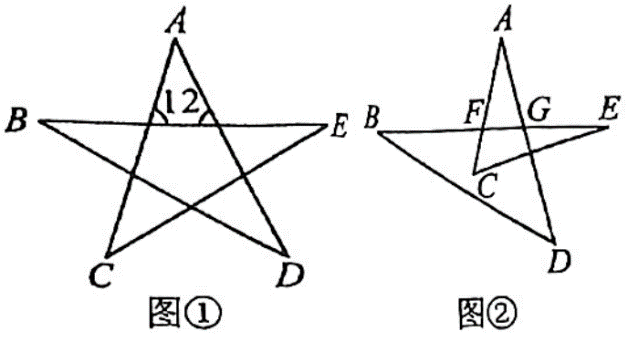(2)、 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E =$ $+ ∠ 1 + ∠ 2 =$ ；

(3)、【应用】
如图②．求 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E$ 的度数．

查看试题解析
14. 小明在计算一个多边形的内角和时，因粗心多加了一个外角，计算出的结果是1506°，请你求出这是一个几边形？并且至少有一个内角是多少度？

查看试题解析
15. 如图，A ， B分别是 $∠ M O N$ 两边 $O M$ ， $O N$ 上的动点（均不与点O重合）．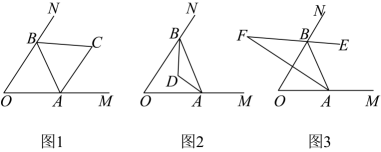

(1)、如图1，当 $∠ M O N = 58 °$ 时， $△ A O B$ 的外角 $∠ N B A$ ， $∠ M A B$ 的平分线交于点C ，则 $∠ A C B =$ $°$ ；

(2)、如图2，当 $∠ M O N = n °$ 时， $∠ O A B$ ， $∠ O B A$ 的平分线交于点D ，则 $∠ A D B =$ $°$ （用含n的式子表示）；

(3)、如图3，当 $∠ M O N = α$ （α为定值， $0 ° < α < 90 °$ ）时， $B E$ 是 $∠ N B A$ 的平分线， $B E$ 的反向延长线与 $∠ O A B$ 的平分线交于点F ．随着点A ， B的运动， $∠ F$ 的大小会改变吗？如果不会，求出 $∠ F$ 的度数（用含α的式子表示）；如果会，请说明理由．

查看试题解析

四、实践探究题（共10分）

16. 阅读下列材料并解答问题：
在一个三角形中，如果一个内角的度数是另一个内角度数的3倍，那么这样的三角形我们称为“3倍角三角形”. 例如：一个三角形三个内角的度数分别是 $12 0^{∘} ， 4 0^{∘} ， 2 0^{∘}$ ，这个三角形就是一个“3倍角三角形”. 反之，若一个三角形是“3倍角三角形”，那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.

(1)、如图①，已知 $∠ M O N = 6 0^{∘}$ ，在射线 $O M$ 上取一点 $A$ ，过点 $A$ 作 $A B ⊥ O M$ 交 $O N$ 于点 $B$ ，判断 $△ A O B$ 是不是“3倍角三角形”，为什么？

(2)、在（1）的条件下，以 $A$ 为端点画射线 $A C$ ，交线段 $O B$ 于点 $C$ （点 $C$ 不与点 $O$ 、点 $B$ 重合），若 $△ A O C$ 是“3倍角三角形”，求 $∠ A C B$ 的度数；

(3)、如图②，点 $D$ 在 $△ A B C$ 的边上，连接 $D C$ ，作 $∠ A D C$ 的平分线交 $A C$ 于点 $E$ ，在 $D C$ 上取一点 $F$ ，使得 $∠ E F C + ∠ B D C = 18 0^{∘} ， ∠ D E F = ∠ B$ ，若 $△ B C D$ 是“3倍角三角形”，求 $∠ B$ 的度数.

查看试题解析