新人教版（2024版）七年级上学期数学第三章质量检测

试卷更新日期：2024-07-03 类型：单元试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 当 $x = 1$ 时， $2 a x^{2} - b x$ 的值为 $- 4$ ，则当 $x = - 2$ 时， $a x^{2} + b x$ 的值为（）．

A、2 B、 $- 2$ C、8 D、 $- 8$

查看试题解析
2. 已知式子 $y^{2} - 2 y + 6$ 的值为 $8$ ，那么式子 $- 2 y^{2} + 4 y + 5$ 的值为（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
3. 设A种糖果的单价为每千克a元，B种糖果的单价为每千克10元，则2千克A种糖果和b千克B种糖果混合而成的什锦糖果的单价为每千克（）

A、 $\frac{a + 10}{2}$ 元 B、 $\frac{2 + b}{2}$ 元 C、 $\frac{2 a + 10 b}{2 + b}$ 元 D、 $\frac{2 a + 10 b}{a + 10}$ 元

查看试题解析
4. 如果|a+2|+(b－1)²=0，那么(a+b)²⁰¹⁹的值等于（）．

A、－1 B、－2019 C、1 D、2019

查看试题解析

二、填空题（每题3分，共15分）

5. x的2倍与y的和用代数式可表示为．

查看试题解析
6. 一个三位数，它的百位数字是 $x$ ，十位数字是 $y$ ，个位数字是 $z$ ，那么这个三位数可以表示为．

查看试题解析
7. 观察下列表格中数组的规律．
组别
数字
等式
1
3，4，5
$3^{2} = 4 + 5$
2
5，12，13
$5^{2} = 12 + 13$
3
7，24，25
$7^{2} = 24 + 25$
4
9，40，41
$9^{2} = 40 + 41$
…
…
…
根据上表的规律，写出第 $n$ 组的三个数字满足的等式：．

查看试题解析

三、解答题（共5题，共37分）

8. 若 $x^{3} - 3 x - 1 = 0$ ，求 $2 x^{3} - 3 x^{2} - 11 x + 8$ 的值．

查看试题解析
9. 若a ， b互为相反数（b不为0），c、d互为倒数，m的绝对值为2，求 $m - c d + \frac{a + b}{2023} + \frac{a}{b}$ 的值．

查看试题解析
10. 已知 $|x + 2| + |y - 3| = 0$ 求 $- \frac{5}{2} x - \frac{5}{3} y + 4 x y$ 的值．

查看试题解析
11. 多多在学习《有理数》这一章时遇到了这样一道趣味题：“四个整数a，b，c，d互不相等，且abcd＝25，求a＋b＋c＋d的值．”多多苦苦思考了很长时间也没有解决，聪明的你能解出答案吗？

查看试题解析
12. 在学习一个数的绝对值过程中，化简|a|时，可以这样分类：当a＞0时，|a|＝a；当a＝0时，|a|＝0；当a＜0时，|a|＝ $-$ a ．请用这种方法解决下列问题．

(1)、当a＝3时，则 $\frac{a}{|a|}$ ＝；当a＝ $-$ 2时，则 $\frac{a}{|a|}$ ＝．

(2)、已知a ， b是有理数，当ab＞0时，试求 $\frac{a}{|a|} + \frac{b}{|b|}$ 的值．

(3)、已知a ， b ， c是非零有理数，满足a+b+c＝0且 $\frac{a}{|a|} + \frac{b}{|b|} + \frac{c}{|c|} ＝$ 1，求 $\frac{b + c}{|a|} + \frac{a + c}{|b|} + \frac{a + b}{|c|}$ 的值．

查看试题解析

四、实践探究题（共3题，共38分）

13. 探索代数式a²-2ab+b²与代数式（a-b）²的关系．

(1)、当a＝2，b＝1时分别计算两个代数式的值．

(2)、当a＝3，b＝-2时分别计算两个代数式的值．

(3)、你发现了什么规律？

(4)、利用你发现的规律计算：2023²-2×2023×2022+2022² ．

查看试题解析
14. 某中学附近的水果超市新进了一批百香果，为了促销这种百香果，特推出两种销售方式
方式一：购买不超过5斤百香果，每斤12元，超出5斤的部分，每斤打8折；
方式二：每斤售价10元．

(1)、顾客买a（a>5）斤百香果，则按照方式一购买需要元；按照方式二购买需要元（请用含a的代数式表示）．

(2)、于老师决定买35斤百香果，通过计算说明用哪种方式购买更省钱．

查看试题解析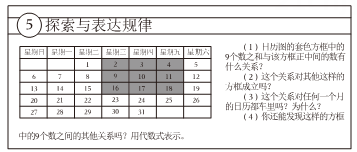
15. 再读教材
请解答教材中的(1)、(2)问。
活学活用
小明是个爱动脑筋的同学，在发现教材中的用方框在月历中移动的规律后，突发奇想，将连续的偶数 $2 ， 4 ， 6 ， 8 ， ⋯$ ，排成如图形式，并用一个十字形框架框住其中的五个数，请你仔细观察十字形框架中的数字的规律，并回答下列问题：

(1)、十字框中的五个数的和与中间的数16有什么关系?

(2)、设中间的数为 $x$ ，用代数式表示十字框中的五个数的和；

(3)、若将十字框上下左右移动，可框住另外的五个数，其它五个数的和能等于2010吗?如能，写出这五个数，如不能，说明理由.

查看试题解析

组别	数字	等式
1	3，4，5	$3^{2} = 4 + 5$
2	5，12，13	$5^{2} = 12 + 13$
3	7，24，25	$7^{2} = 24 + 25$
4	9，40，41	$9^{2} = 40 + 41$
…	…	…