新人教版(2024版)七年级上学期数学第一章质量检测
试卷更新日期:2024-07-03 类型:单元试卷
一、选择题
-
1. 中国空间站位于距离地面约的太空环境中.由于没有大气层保护,在太阳光线直射下,空间站表面温度可高于零上 , 其背阳面温度可低于零下 . 若零上记作 , 则零下记作( )A、 B、 C、 D、2. 实数m,n在数轴上对应的点的位置如图所示,若mn<0,且|m|<|n|,则原点可能是( )
 A、点A B、点B C、点C D、点D3. 一种大米的质量标识为“(50±0.3)千克”,则下列各袋大米中质量不合格的是( )A、50.0千克 B、50.3千克 C、49.7千克 D、49.6千克4. 已知点A,B,C,D在数轴上的位置如图所示,且相邻两点之间的距离均为1个单位长度.若点A,B,C,D分别表示数 , b,c,d,且满足 , 则b的值为( )
A、点A B、点B C、点C D、点D3. 一种大米的质量标识为“(50±0.3)千克”,则下列各袋大米中质量不合格的是( )A、50.0千克 B、50.3千克 C、49.7千克 D、49.6千克4. 已知点A,B,C,D在数轴上的位置如图所示,且相邻两点之间的距离均为1个单位长度.若点A,B,C,D分别表示数 , b,c,d,且满足 , 则b的值为( )
 A、 B、 C、 D、5. 若 , 则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、5. 若 , 则的取值范围是( )A、 B、 C、 D、二、填空题
-
6. 有理数a,b,c都不为零,且a+b+c=0,则= .
三、解答题
-
7. 把下列各数填在相应的集合中:8,-1,-0.4, , 0, , , , .
正数集合{ ▲ …};
负数集合{ ▲ …};
整数集合{ ▲ …};
分数集合{ ▲ …};
非负有理数集合{ ▲ …}.
8. 某检修小组开车从单位出发,检修东西走向的供电线路,规定向东为正,向西为负,一天的行程是(单位:千米): , , , , , , 4, , 16, .(1)、最后他们是否回到出发点?若没有,则在出发点的什么方向?距离出发点多远?(2)、若汽车耗油量为升千米,检修小组完成工作返回出发地,则他们该天共耗油多少升?9. 在数轴上表示下列各数,并用“<”符号将它们连接起来.-4,|-2.5|,-|3|,-1 , -(-1),0
10.
已知 .(1)、求 , 的值;(2)、已知 , 求的值四、综合题
-
11. 如图.在一条不完整的数轴上一动点A向左移动4个单位长度到达点B,再向右移动7个单位长度到达点C,
 (1)、若点A表示的数为0,求点B、点C表示的数;(2)、若点C表示的数为5,求点B、点A表示的数;(3)、如果点A、C表示的数互为相反数,求点B表示的数.12. 如图,将一根木棒放在数轴(单位长度为)上,木棒左端与数轴上的点重合,右端与数轴上的点重合.
(1)、若点A表示的数为0,求点B、点C表示的数;(2)、若点C表示的数为5,求点B、点A表示的数;(3)、如果点A、C表示的数互为相反数,求点B表示的数.12. 如图,将一根木棒放在数轴(单位长度为)上,木棒左端与数轴上的点重合,右端与数轴上的点重合.
 (1)、若将木棒沿数轴向右水平移动,则当它的左端移动到点时,它的右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它的右端移动到点时,它的左端在数轴上所对应的数为3,由此可得这根木棒的长为;(2)、图中点所表示的数是 , 点所表示的数是;(3)、受(1)(2)的启发,请借助“数轴”这个工具解决下列问题:
(1)、若将木棒沿数轴向右水平移动,则当它的左端移动到点时,它的右端在数轴上所对应的数为30;若将木棒沿数轴向左水平移动,则当它的右端移动到点时,它的左端在数轴上所对应的数为3,由此可得这根木棒的长为;(2)、图中点所表示的数是 , 点所表示的数是;(3)、受(1)(2)的启发,请借助“数轴”这个工具解决下列问题:一天,小明去问爷爷的年龄,爷爷说:“我若是你现在这么大,你还要37年才出生;你若是我现在这么大,我就119岁啦!”求爷爷和小明的年龄.

五、实践探究题
-
13. 综合探究
阅读材料:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
如图 , 在数轴上有理数对应的点为点 , 有理数对应的点为点 , , 两点之间的距离表示为或 , 记为 .
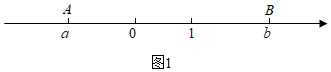 (1)、解决问题:数轴上有理数与对应的两点之间的距离等于;数轴上有理数与对应的两点之间的距离用含的式子表示为;若数轴上有理数与对应的两点 , 之间的距离 , 则等于;(2)、联系拓广如图 , 点 , , 是数轴上的三点,点表示的数为 , 点表示的数为 , 动点表示的数为 .
(1)、解决问题:数轴上有理数与对应的两点之间的距离等于;数轴上有理数与对应的两点之间的距离用含的式子表示为;若数轴上有理数与对应的两点 , 之间的距离 , 则等于;(2)、联系拓广如图 , 点 , , 是数轴上的三点,点表示的数为 , 点表示的数为 , 动点表示的数为 .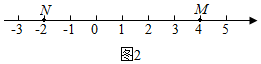
若点在点 , 之间,则 .
若 , 即点到点的距离等于点到点距离的倍,则等于 .
能力提升:若点在点 , 之间,则 .
若 , 则等于 .
14. 探索下列问题:(可根据来解决问题)(1)、若有最小值,则当时,有最小值为.(2)、当m取何值时,有最小值,最小值为多少?(3)、当m取何值时,有最大值,最大值为多少?
-