【培优版】北师大版数学八上1.1探究勾股定理 同步练习
试卷更新日期:2024-07-02 类型:同步测试
一、选择题
-
1. 如图,在矩形中, , . 点是边上一点,将沿所在直线折叠,使得点恰好落在边上点处,则的长是( )
 A、 B、 C、 D、2. 如图,两个全等的矩形AEFG,矩形ABCD如图所示放置.CD所在直线与AE,GF分别交于点H,M.若AB=3,BC= ,CH=MH.则线段MH的长度是( )
A、 B、 C、 D、2. 如图,两个全等的矩形AEFG,矩形ABCD如图所示放置.CD所在直线与AE,GF分别交于点H,M.若AB=3,BC= ,CH=MH.则线段MH的长度是( ) A、 B、 C、 D、23. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )
A、 B、 C、 D、23. 如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( ) A、4 B、6 C、10 D、164. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A、4 B、6 C、10 D、164. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )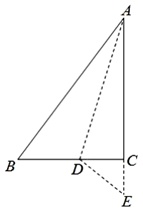 A、1cm B、cm C、cm D、2cm5. 如图,在中, , BC的垂直平分线分别交AB , BC于点D , E . 若 , 则的周长为( )
A、1cm B、cm C、cm D、2cm5. 如图,在中, , BC的垂直平分线分别交AB , BC于点D , E . 若 , 则的周长为( ) A、13 B、17 C、18 D、306. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、157. 如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( )
A、13 B、17 C、18 D、306. 已知a、b为两正数,且 ,则代数式 最小值为( )A、12 B、13 C、14 D、157. 如图,在矩形ABCD中,AB=12,BC=16,将矩形ABCD沿EF折叠,使点B与点D重合,则折痕EF的长为( ) A、14 B、 C、 D、158. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
A、14 B、 C、 D、158. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )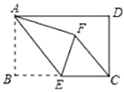 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如图,中, , 于点 , 平分 , 交与点 , 于点 , 且交于点 , 若 , , 则 .
 10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上的一动点(不包含A,B两端点),沿CD折叠,点A落在点A'处,A'C与AB相交于点E若A'D∥BC,则A'E的长为。
10. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上的一动点(不包含A,B两端点),沿CD折叠,点A落在点A'处,A'C与AB相交于点E若A'D∥BC,则A'E的长为。 11. 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,下列结论:①∠DIF=45°;②CF
11. 如图,△ABC中,∠A=90°,角平分线BD、CE交于点I,IF⊥CE交CA于F,下列结论:①∠DIF=45°;②CF
+BE=BC;③若AB=3,AC=4,则.其中正确的是 . 12. 如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.若D为AB中点,AB=13,BC=10,求CE= , AF=.
12. 如图,在△ABC中,AB=AC,∠A<90°,点D,E,F分别在边AB,BC,CA上,连接DE,EF,FD,已知点B和点F关于直线DE对称.若D为AB中点,AB=13,BC=10,求CE= , AF=. 13. 在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是 , , , , 则 .
13. 在直线上依次摆着七个正方形(如图),已知斜放置的三个正方形的面积分别为1,2,3,正放置的四个正方形的面积是 , , , , 则 .

三、解答题
-
14. 如图,已知AB=12,AB⊥BC于B,AB⊥AD于A,AD=5,BC=10点E是CD的中点,求AE的长.
 15. 如图,中, , D为中点,点E在直线上(点E不与点B , C重合),连接 , 过点D作交直线于点F , 连接 .
15. 如图,中, , D为中点,点E在直线上(点E不与点B , C重合),连接 , 过点D作交直线于点F , 连接 . (1)、如图1,当点F与点A重合时,请直接写出线段与的数量关系: .(2)、如图2,当点F不与点A重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , , 请直接写出线段AF的长.16. 如图,矩形中, , , 为上一点,将沿翻折至 , 与相交于点 , 与相交于点 , 且 , 求的长.
(1)、如图1,当点F与点A重合时,请直接写出线段与的数量关系: .(2)、如图2,当点F不与点A重合时,请写出线段 , , 之间的数量关系,并说明理由;(3)、若 , , , 请直接写出线段AF的长.16. 如图,矩形中, , , 为上一点,将沿翻折至 , 与相交于点 , 与相交于点 , 且 , 求的长.

