【提升版】北师大版数学八上1.1探究勾股定理 同步练习
试卷更新日期：2024-07-02 类型：同步测试
一、选择题
-
1. 如图，图中每个四边形都是正方形，字母A所代表的正方形的面积为（ ）
A、4 B、8 C、16 D、642. 如图，以Rt△ABC为直径分别向外作半圆，若S1＝10，S3＝8，则S2＝（ ）
A、2 B、6 C、 D、3. 满足下列条件的△ABC不是直角三角形的是（ ）A、AC＝1，BC＝ ，AB＝2 B、AC：BC：AB＝3：4：5 C、∠A：∠B：∠C＝1：2：3 D、∠A：∠B：∠C＝3：4：54. 在锐角中， ， ， 高 ， 则BC的长度为（ ）A、16 B、15 C、14 D、135. 如图是一个正方形和直角三角形的组合图形，直角三角形的斜边和一条直角边的长分别为10cm，8cm，则该正方形的面积为（ ）
A、6cm2 B、36cm2 C、18cm2 D、2cm26. 如图，有一张直角三角形纸片，两直角边长AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD等于（ ）
A、 cm B、 cm C、 cm D、 cm7. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时， 梯子底端到左墙角的距离BC为0.7m，梯子顶端到地面的距离AC为2.4m．如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A'D为1.5m，则小巷的宽为（ ）．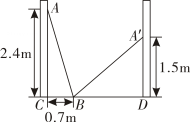
A、2.4m B、2m C、2.5m D、2.7m8. 《九章算术》内容丰富，与实际生活联系紧密，在书上讲述了这样一个问题“今有垣高一丈，倚木于垣，上与垣齐.引木却行一尺，其木至地.问木长几何？”其内容可以表述为：“有一面墙，高一丈.将一根木杆斜靠在墙上，使木杆的上端与墙的上端对齐，下端落在地面上.如果使木杆下端从此时的位置向远离墙的方向移动1尺，则木杆上端恰好沿着墙滑落到地面上.问木杆长多少尺？”（说明：1丈＝10尺）设木杆长x尺，依题意，下列方程正确的是（ ）A、x2＝（x﹣1）2+102 B、（x+1）2＝x2+102 C、x2＝（x﹣1）2+12 D、（x+1）2＝x2+12二、填空题
-
9. 如图， ．
10. 如图，在中， ， 分别以 ， 为边长向外作正方形，且它们的面积分别为9和25，则的长为 ．
11. 如图1，第24届国际数学家大会会标是以我国古代数学家赵爽的弦图为基础进行设计的．现假设可在如图2的弦图区域内随机取点，若正方形中， ， 则这个点落在阴影部分的概率为 ．
12. 如图，矩形纸片ABCD中，BC＝8cm ， 把矩形纸片沿直线BD折叠，点C落在点E处，BE交AD于点F ， 若BF＝cm ， 则CD的长度为 ．
13. 如图．将矩形ABCD沿直线DE折叠，顶点A落在BC边上F处，已知BE＝3，CD＝8．则BF的长是 ．
三、解答题
-
14. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C＇处，BC交AD于E，AD=8，AB=4，求DE的长.
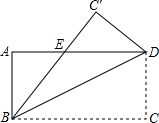15. 如图，花果山上有两只猴子在一棵树 上的点B处，且 ，它们都要到A处吃东西，其中一只猴子甲沿树爬下走到离树 处的A处，另一只猴子乙先爬到项D处后再沿缆绳 滑到A处.已知两只猴子所经过的路程相等，设 为 .求这棵树高有多少米?
16. 求如图的Rt△ABC的面积.
17. 在△ABC中，AB=AC，D是BC延长线上的点，求证：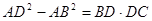
. 四、综合题
-
18. 阅读下列内容：设a，b，c是一个三角形的三条边的长，且a是最长边，我们可以利用a，b，c三条边长度之间的关系来判断这个三角形的形状：①若 ，则该三角形是直角三角形；②若 ，则该三角形是钝角三角形；③若 ，则该三角形是锐角三角形.例如：若一个三角形的三边长分别是4，5，6，则最长边是6， ，故由③可知该三角形是锐角三角形，请解答以下问题：(1)、若一个三角形的三边长分别是7，8，9，则该三角形是三角形.(2)、若一个三角形的三边长分别是5，12，x，且这个三角形是直角三角形，求 的值.