新人教版数学七上复习：整式加减运算的实际应用

试卷更新日期：2024-07-02 类型：复习试卷

进入出卷网下载

一、选择题

1. 某学校图书馆周三下午有 $(a + 3 b - 2)$ 位同学，七年级组织 $(a + 3)$ 位同学来图书馆阅读，后来有 $(a + 2 b + 1)$ 位同学因上课要离开，那么图书馆内还剩下的同学数为（）

A、 $a + 2 b$ B、 $2 a + b$ C、 $a + b$ D、 $a + b + 1$

查看试题解析
2. 小明爸爸的服装店经销一种服装，进货价为每件a元，小明爸爸先将进货价提高80%进行标价，销售情况不够理想．元旦前夕小明爸爸决定进行降价销售，按标价的七折销售，结果全部售出那么元旦卖出的服装每件（）

A、比进货价便宜了 $0.26 a$ 元 B、比进货价高了 $0.26 a$ 元 C、比进货价便宜了 $0.3 a$ 元 D、与进货价相同

查看试题解析
3. 某初中七年级学生人数为a人，八年级人数比七年级人数的 $\frac{2}{3}$ 多10人，九年级人数比八年级人数的2倍少60人，用含a的式子表示这个学校的总人数（单位：人）为（）

A、 $3 a$ B、 $\frac{11}{3} a - 40$ C、 $3 a - 40$ D、 $3 a - 30$

查看试题解析
4. 某商店在甲批发市场以每盒m元的进价购进40盒中性笔，又在乙批发市场以每盒n元（ $m > n$ ）的进价购进同样的60盒中性笔，如果该商店以每盒 $\frac{m + n}{2}$ 元的售价卖出这种中性笔，卖完后，这家商店（）

A、盈利了 B、亏损了 C、不盈不亏 D、盈亏不能确定

查看试题解析
5. 小明在超市买回若干个相同的纸杯，他把纸杯整齐地叠放在一起．如图①，3个纸杯的高度为11cm ，如图②，5个纸杯的高度为13cm ，若把n个这样的杯子叠放在一起，高度为（　　）cm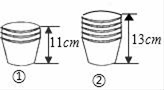

A、n+10 B、n+8 C、2n+5 D、2n+3

查看试题解析
6. 两艘船从同一港口出发，甲船顺水而下，乙船逆水而上，已知两船在静水中的速度都是45km/h，水流速度是akm/h，1h后两船相距（）km.

A、90 B、4a C、2a D、180

查看试题解析
7. 如图，把四张形状大小完全相同的小长方形卡片(如图1)，不重叠地放在一个长为 $a c m$ 、宽为 $b c m$ 长方形内(如图2)，未被卡片覆盖的部分用阴影表示，则图2中两块阴影部分的周长和是（）

A、 $4 a c m$ B、 $4 b c m$ C、 $2 (a + b) c m$ D、 $4 (a - b) c m$

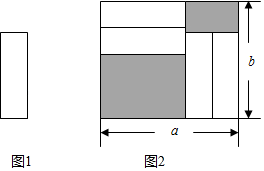查看试题解析
8. 如图，某长方形花园的长为(x+y)米，宽为(x-y)米．现根据实际需要对该花园进行整改，长方形花园的长增加(x-y)米，宽增加(x- 2y)米，则整改后该花园的周长为（）

A、(4x-3y)米 B、(4x- 6y)米 C、(8x-3y)米 D、(8x-6y)米

查看试题解析
9. 在长方形ABCD内，将两张边长分别为a和 $b (a > b)$ 的正方形纸片按图①，②两种方式放置（图①，②中两张正方形纸片均有部分重叠），长方形中未被这两张正方形纸片覆盖的部分用阴影表示.若 $A D = m ， A B = n$ ，图①中阴影部分的面积表示为 $S_{1}$ ，图②中阴影部分的面积表示为 $S_{2}$ ， $S_{2} - S_{1}$ 的值与a，b，m，n四个字母中哪个字母的取值无关（）

A、与a的取值无关 B、与b的取值无关 C、与m的取值无关 D、与n的取值无关.

查看试题解析
10. 现有1张大长方形和3张相同的小长方形卡片，按如图所示两种方式摆放，则小长方形的长与宽的差是（）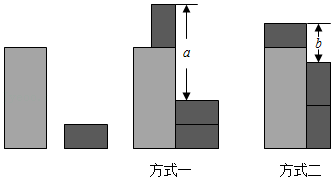

A、a-b B、 $\frac{a - b}{2}$ C、 $\frac{a - b}{3}$ D、 $\frac{a + b}{3}$

查看试题解析

二、填空题

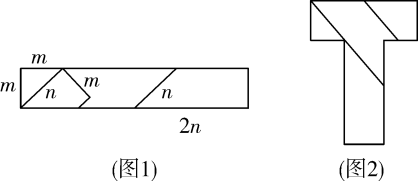
11. 2022年11月3 日，中国空间站“T”字基本构型在轨组装完成，“T”寓意：睿智，卓越．图1是用长方形纸板做成的四巧板(已知线段长度如图所示)，用它拼成图2的“T”字型图形，则“T”字型图形的周长为． (用含m，n的式子表示)

查看试题解析
12. 一辆客车上原有 $(6 a - 2 b)$ 人，中途下车一半人数，又上车若干人，这时车上共有 $(12 - 5 b)$ 人．则中途上车的乘客是人．

查看试题解析
13. 现有三堆棋子，数目相等，每堆至少有4枚. 从左堆中取出3枚放入中堆，从右堆中取出4枚放入中堆，再从中堆中取出与左堆剩余棋子数相同的棋子数放入左堆，这时中堆的棋子数是枚.

查看试题解析
14. 如图，由一块正方形地和一块长方形地组成的花园，分别以正方形的边长为半径画圆弧，以长方形的长为直径画圆弧，如图所示．园艺师准备在阴影部分种花，则阴影部分的种植面积为平方米？（用含a的代数式表示，结果保留π）．

查看试题解析
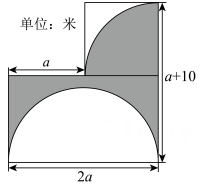15. 一件商品每件成本 $a$ 元，原来按成本价增加22%定出价格，现在由于库存积压减价，按原价打八五折出售，现在每件可以盈利元.

查看试题解析

三、解答题

16. 有一个关于猜数的游戏如下：游戏甲方把自己的出生月份数乘2，加10，把所得的和乘5，再加上他家的人口数(小于10)，将结果告诉游戏乙方，乙方就能猜出甲方出生的月份和他家的人口数．
你能用代数式的知识来解释这个游戏的原理吗？

查看试题解析
17. A、B、C．D四个车站的位置如图所示，车站B距车站A、D的距离分别为 $(a + b) k m$ 、 $(5 a + 36) k m$ ，车站C与车站D的距离为 $(3 a + 2 b) k m$ ．其中a，b是不为0的实数．

(1)、求B、C两站之间的距离（用含a、b的代数式表示）．

(2)、若B、D两个车站之间的距离比A、B两个车站之间的距离长8km，求出B、C两个车站相距多少km？

查看试题解析
18. 绿源超市销售茶壶、茶杯，茶壶每只定价50元，茶杯每只定价6元．春节期间，超市将开展促销活动，向顾客提供两种优惠方案：
方案一：每买一只茶壶就赠一只茶杯；
方案二：茶壶和茶杯都按定价的90%付款．
某顾客计划到该超市购买茶壶8只和茶杯x只（茶杯数多于8只）．

(1)、用含x的代数式分别表示方案一与方案二各需付款多少元？

(2)、当 $x = 15$ 时，请通过计算说明该顾客选择上面的两种购买方案哪种更省钱？

查看试题解析
19. 如图是由正奇数排成的数阵：

(1)、请计算图中“工”形框中七个数的和是中间数45的几倍；

(2)、在数阵中任意做一个这样的“工”形框，（1）中的关系是否仍成立?并写出理由；

(3)、用这样的“工”形框能框出和为2023的七个数吗?如果能，求出这七个数中间的数；如果不能，请写出理由．

查看试题解析
20. 如图，某公园有一块长为 $(2 a - 1)$ 米，宽为 $a$ 米的长方形土地，现将三面留出宽都是 $x$ 米的小路，余下的部分设计成花圃种植名贵花草，并用篱笆把四周围起来．

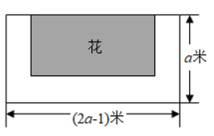(1)、用代数式表示所用篱笆的总长度；

(2)、当 $a = 11$ ， $x = 0.8$ 时，求所用篱笆的总长度．

查看试题解析
21. 学校体育室有两个球筐，已知甲筐内的球比乙筐内球的个数的3倍还多5个．现进行如下操作：第一次，从甲筐中取b球放入乙筐：第二次，又从甲筐取出若干个球放入乙筐，这次取出的球的个数是第一次操作后乙筐内球的个数的2倍．若设乙筐内原来有a个球，两次操作后，某同学将甲、乙两筐内球的个数整理如表：
球的个数/
操作前后
甲筐内球的个数
乙筐内球的个数
操作前
①
a
第一次操作后
3a﹣b+5
a+b
第二次操作后
②
3a+3b

(1)、在表格中，①处代数式为， ②处代数式为；（用含a、b的式子表示）

(2)、当a＝4，b＝2时，第二次操作后，甲筐比乙筐内球的个数多还是少，多或少几个球？

查看试题解析
22. 做大小两个长方体纸盒，尺寸如下（单位：cm）：

长
宽
高
小纸盒
a
b
c
大纸盒
1.5a
2b
2c

(1)、1个小纸盒的表面积是cm² ， 1个大纸盒的表面积是cm²（用含a，b，c的式子表示）；

(2)、求做这样的2个小纸盒和1个大纸盒共用料多少平方厘米？（用含a，b，c的式子表示）

(3)、求做这样的1个大纸盒比做这样的1个小纸盒多用料多少平方厘米？（用含a，b，c的式子表示）

查看试题解析
23. 近年来，电商多选择在11月11日促销．今年的促销期间，某电商客服在为买家包装商品时用到长、宽、高分别为a厘米、b厘米、c厘米的箱子，并发现有如图所示的乙两种打包方式（打包带不计接头处的长）．回答下列问题：

(1)、用含a，b， c的式子表示甲、乙两种打包方式所用的打包带的长度：
甲需要厘米，乙需要厘米；

(2)、当a=50厘米，b=40厘米，c=30厘米时，直接写出甲、乙两种打包方式所用的打包带的长度：甲需要厘米，乙需要厘米；

(3)、当a>b>c时，两种打包方式中，哪种方式节省打包带？并说明你的理由．

查看试题解析
24. 当你记不住九九乘法表中乘9的口诀是，你可以进行如下的操作：例如，伸出两只手，做运算 $4 \times 9$ 时，如图，从左手开始数4下，数到第4根手指向下弯．这时，如图1该手指左边有3根手指，右边有6根手指，可得36，即 $4 \times 9 = 36$ ．类似的，做运算 $8 \times 9$ 时，从左手开始数8下，数到第8根手指向下弯，这时，该手指左边有7根手指，右边有2根手指，可得72，即 $8 \times 9 = 72$ ． $⋅ ⋅ ⋅$

(1)、在计算 $6 \times 9$ 时，从左手开始数，数到第根手指向下弯下，这时，该手指左边有根手指，右边有根手指；

(2)、将问题一般化，我们可以解决 $9 n$ （ $1 ≤ n ≤ 9$ ，且 $n$ 为整数）的问题．从左手开始数 $n$ 下，数到第 $n$ 根手指向下弯，此时该手指左边有根手指，右边有根手指，由此即可得 $9 n =$ ；

(3)、小郭同学在研究的过程中发现，若 $n$ 是一个特殊两位数时，如 $12 ， 34 ， 45$ 等，当这样的两位数与9相乘时，也能够通过指算法求解．如图2是 $12 \times 9 = 108$ 的指算法过程，假设 $m$ 是这个两位数的个位数字，请用含有 $m$ 的等式表示上述规律，并说明它的正确性．

查看试题解析

球的个数/ 操作前后	甲筐内球的个数	乙筐内球的个数
操作前	①	a
第一次操作后	3a﹣b+5	a+b
第二次操作后	②	3a+3b

	长	宽	高
小纸盒	a	b	c
大纸盒	1.5a	2b	2c