【培优版】新北师大版(2024)数学七上2.1认识有理数同步练习

试卷更新日期：2024-07-02 类型：同步测试

进入出卷网下载

一、选择题

1. 已知a，b，c为非零的实数，且不全为正数，则 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ 的所有可能结果的绝对值之和等于（）

A、5 B、6 C、7 D、8

查看试题解析
2. 若 $2 a + b = 0 (a \neq 0)$ ，则 $\frac{a}{| b |} + \frac{| a |}{b} - 1$ 的值为（）

A、0或1 B、 $- 1$ 或0 C、 $- 1$ D、 $- 2$

查看试题解析
3. 如图，是正方体包装盒的表面积展开图，如在其中的三个正方形 $A$ 、 $B$ 、 $C$ 、 $D$ 内分别填上适当的数，使得将这个表面积展开图沿虚线折成正方形后，相对面上的两数字互为相反数，则填在 $A$ 、 $B$ 、 $C$ 内的三个数字依次为（）

A、0，1，-2 B、0，-2，1 C、1，0，-2 D、-2，0，1

查看试题解析
4. 已知： $m = \frac{| a + b |}{c} + \frac{2 | b + c |}{a} + \frac{3 | c + a |}{b}$ ，且 $a b c > 0$ ， $a + b + c = 0 .$ 则 $m$ 共有 $x$ 个不同的值，若在这些不同的 $m$ 值中，最大的值为 $y$ ，则 $x + y =$ （）

A、 $4$ B、 $3$ C、 $2$ D、 $1$

查看试题解析
5. 代数式 $| x + 9 | + | x - 5 |$ 的最小值是（）

A、 $0$ B、 $9$ C、 $14$ D、 $15$

查看试题解析
6. 如图，圆的周长为4个单位长度．在该圆的4等分点处分别标上0、1、2、3，先让圆周上表示数字0的点与数轴上表示-1的点重合，再将数轴按逆时针方向环绕在该圆上．则数轴上表示2013的点与圆周上表示数字（）的点重合．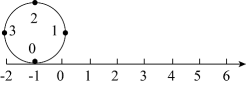

A、0 B、1 C、2 D、3

查看试题解析
7. 若a是负数，且|a|<1，则 $\frac{|a - 1|}{|a| - 1}$ 的值是（）

A、等于1 B、大于-1，且小于0 C、小于-1 D、大于1

查看试题解析

8. 下面的五个时钟显示了同一时刻国外四个城市的时间和北京时间，若下表给出的是国外四个城市与北京的时差，则这四个时钟对应的国外城市从左到右依次是（）

城市	时差/h
纽约	﹣13
悉尼	+2
伦敦	﹣8
罗马	﹣7

A、伦敦、纽约、罗马、悉尼 B、罗马、悉尼、伦敦、纽约 C、纽约、悉尼、伦敦、罗马 D、罗马、伦敦、悉尼、纽约

查看试题解析

二、填空题

9. 若a，b，c为整数，且|a－b|＋|c－a|＝1，则|c－a|＋|a－b|＋|b－c|的值为

查看试题解析
10. 同学们都知道： $| 5 - (- 2) |$ 表示5与-2之差的绝对值，实际上也可理解为5与-2两数在数轴上所对应的两点之间的距离，同理， $| x + 2 | + | x + 3 |$ 可以表示数轴上有理数 $x$ 所对应的点到-2和-3所对应的点的距离之和，则 $| x + 2 | + | x + 3 |$ 的最小值为.

查看试题解析
11. 如图，在数轴上，点B在点A的右侧．已知点A 对应的数为 $- 1$ ，点B对应的数为m，点C到原点的距离为2，且 $A C + B C = 5$ ，则m的值为．

查看试题解析
12. 若 $| x | + 3 = | x - 3 |$ ，则x的取值范围是．

查看试题解析
13. 若|m﹣2|+|n+3|=0，则m+n= ．

查看试题解析

三、解答题

14. 如图在数轴上A点表示数 $a$ ， $B$ 点表示数 $b$ ， $a$ 、 $b$ 满足 $| a + 2 | + | b - 4 | = 0$ ；

(1)、点A表示的数为；点 $B$ 表示的数为；

(2)、若在原点 $O$ 处放一挡板，一小球甲从点A处以 $1$ 个单位 $/$ 秒的速度向左运动；同时另一小球乙从点 $B$ 处以 $2$ 个单位 $/$ 秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，设运动的时间为 $t （$ 秒 $）$ ，
$①$ 当 $t = 1$ 时，甲小球到原点的距离 $=$ ▲ ；乙小球到原点的距离 $=$ ▲ ；
当 $t = 3$ 时，甲小球到原点的距离 $=$ ▲ ；乙小球到原点的距离 $=$ ▲ ；
$②$ 试探究：甲，乙两小球到原点的距离可能相等吗？若不能，请说明理由．若能，请直接写出甲，乙两小球到原点的距离相等时经历的时间．

查看试题解析
15. 在学习绝对值后，我们知道，|a|表示数a在数轴上的对应点与原点的距离．如：|5|表示5在数轴上的对应点到原点的距离．而|5|=|5﹣0|，即|5﹣0|表示5、0在数轴上对应的两点之间的距离．类似的，有：|5﹣3|表示5、3在数轴上对应的两点之间的距离；|5+3|=|5﹣（﹣3）|，所以|5+3|表示5、﹣3在数轴上对应的两点之间的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a﹣b|．
请根据绝对值的意义并结合数轴解答下列问题：

(1)、数轴上表示2和3的两点之间的距离是；数轴上P、Q两点的距离为3，点P表示的数是2，则点Q表示的数是．

(2)、点A、B、C在数轴上分别表示有理数x、﹣3、1，那么A到B的距离与A到C的距离之和可表示为（用含绝对值的式子表示）；满足|x﹣3|+|x+2|=7的x的值为．

(3)、试求|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣100|的最小值．

查看试题解析

16. 如图，甲、乙两人（看成点）分别在数轴

- 6

和9的位置上，沿数轴做移动游戏．移动游戏规则：两人先进行“石头、剪刀、布”，而后根据输赢结果进行移动．

①若平局，则甲向东移动1个单位长度，同时乙向西移动1个单位长度；

②若甲赢，则甲向东移动5个单位长度，同时乙向东移动3个单位长度；

③若乙赢，则甲向西移动3个单位长度，同时乙向西移动5个单位长度．

前三局如下表：（提示：剪刀胜布，布胜石头，石头胜剪刀）

	第一局	第二局	第三局…
甲的手势	石头	剪刀	石头	…
乙的手势	石头	布	布	…

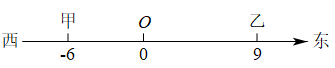(1)、从如图所示的位置开始，求第一局后甲、乙两人分别在数轴上的位置．

(2)、从如图所示的位置开始，从前三局看，第几局后甲离原点最近，离原点距离多少？

(3)、从如图所示的位置开始，若进行了k局后，甲与乙的位置相距3个单位长度，请直接写出k的值．

查看试题解析

17. 绝对值拓展材料：|a|表示数a在数轴上的对应点与原点的距离．如：|5|表示5在数轴上的对应点到原点的距离．而|5|＝|5-0|，即|5-0|表示5、0在数轴上对应的两点之间的距离．类似的，有：|5+3|＝|5-（-3）|表示5、-3在数轴上对应的两点之间的距离．一般地，点A、B在数轴上分别表示有理数a、b，那么A、B之间的距离可表示为|a-b|．完成下列题目：

(1)、A、B分别为数轴上两点，A点对应的数为-2，B点对应的数为4．
①A、B两点之间的距离为．
②折叠数轴，使A点与B点重合，则表示-3的点与表示的点重合；
③若在数轴上存在一点P到A的距离是点P到B的距离的2倍，则点P所表示的数是．

(2)、若满足|x-1|+|x+5|＝8时，则x的值是．

(3)、求|x-2|+|x+2|+|x+3|的最小值为，此时x的值为．

查看试题解析
18. 阅读下列材料并解决有关问题：我们知道 $| x | = {\begin{array}{l} x \\ 0 \\ - x \end{array} \begin{array}{l} ， \\ ， \\ ， \end{array} \begin{array}{l} (x > 0) \\ (x = 0) \\ (x < 0) \end{array}$ ，所以当 $x > 0$ 时， $\frac{x}{| x |} = \frac{x}{x} = 1$ ；当 $x < 0$ 时， $\frac{x}{| x |} = \frac{x}{- x} = - 1$ ，现在我们可以用这个结论来解决下面问题：

(1)、已知 $a$ ， $b$ 是有理数，当 $a b \neq 0$ 时，求 $\frac{a}{| a |} + \frac{b}{| b |}$ 的值；

(2)、已知 $a$ ， $b$ ， $c$ 是有理数，当 $a b c \neq 0$ ，求 $\frac{a}{| a |} + \frac{b}{| b |} + \frac{c}{| c |}$ 的值；

(3)、已知 $a$ ， $b$ ， $c$ 是有理数， $a + b + c = 0$ ， $a b c < 0$ ，求 $\frac{b + c}{| a |} + \frac{a + c}{| b |} + \frac{a + b}{| c |}$ 的值.

查看试题解析

【培优版】新北师大版(2024)数学七上2.1认识有理数 同步练习

一、选择题

二、填空题

三、解答题

【培优版】新北师大版(2024)数学七上2.1认识有理数同步练习