人教版九年级上学期数学课时进阶测试22.3实际问题与二次函数(三 阶)
试卷更新日期:2024-07-02 类型:同步测试
一、选择题
-
1. 如图 和 都是边长为2的等边三角形,它们的边 在同一条直线l上,点C,E重合,现将 沿着直线l向右移动,直至点B与F重合时停止移动.在此过程中,设点移动的距离为x,两个三角形重叠部分的面积为y,则y随x变化的函数图象大致为( )
 A、
A、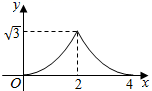 B、
B、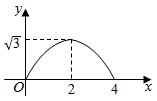 C、
C、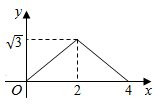 D、
D、 2. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
2. 如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )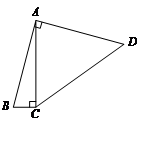
A、 B、 C、 D、3. 如图,抛物线y=﹣x2+2x+m+1交x轴于点A(a , 0)和B(b , 0),交y轴于点C , 抛物线的顶点为D , 下列四个命题:①当x>0时,y>0; ②若a=﹣1,则b=4;③抛物线上有两点P(x1 , y1)和Q(x2 , y2),若x1<1<x2 , 且x1+x2>2,则y1>y2;
④点C关于抛物线对称轴的对称点为E , 点G , F分别在x轴和y轴上,当m=2时,四边形EDFG周长的最小值为 . 其中真命题的序号是( )
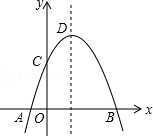 A、① B、② C、③ D、④4. 下面的三个问题中都有两个变量:
A、① B、② C、③ D、④4. 下面的三个问题中都有两个变量:①将一根长为的铁丝刚好围成一个矩形,矩形的面积y与矩形一条边长x;
②赵老师匀速从家走到学校所走的路程y和行走时间x;
③中秋节后,某超市月饼卖不出去,决定促销,月饼成本价为10元/kg , 原价为30元/kg , 此时日销量为10kg , 当月饼单价每降价1元,每天可以多卖出10kg , 月饼利润y与降价x;其中,变量y与变量x之间的函数关系可以用如图所示的图像表示的( )
 A、① B、①③ C、②③ D、①②③5. 如图,在平面直角坐标系中,平行于x轴的直线 , 与二次函数 , 分别交于A、B和C、D , 若 , 则a为( )
A、① B、①③ C、②③ D、①②③5. 如图,在平面直角坐标系中,平行于x轴的直线 , 与二次函数 , 分别交于A、B和C、D , 若 , 则a为( ) A、4 B、2 C、 D、6. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )A、 B、 C、 D、7. 如图,垂直于x轴的直线AB分别与抛物线C1:和抛物线C2:交于A,B两点,过点A作CD//x轴分别与y轴和抛物线C2交于点C,D,过点B作EF//x轴分别与y轴和抛物线C1交于点E,F,则的值为( )
A、4 B、2 C、 D、6. “抖音直播带货”已经成为一种热门的销售方式,某抖音主播代销某一品牌的电子产品(这里代销指厂家先免费提供货源,待货物销售后再进行结算,未售出的由厂家负责处理).销售中发现每件售价99元时,日销售量为200件,当每件电子产品每下降5元时,日销售量会增加10件.已知每售出1件电子产品,该主播需支付厂家和其他费用共50元,设每件电子产品售价为x(元),主播每天的利润为w(元),则w与x之间的函数解析式为( )A、 B、 C、 D、7. 如图,垂直于x轴的直线AB分别与抛物线C1:和抛物线C2:交于A,B两点,过点A作CD//x轴分别与y轴和抛物线C2交于点C,D,过点B作EF//x轴分别与y轴和抛物线C1交于点E,F,则的值为( ) A、 B、 C、 D、8. 学校组织学生去绍兴进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且喷口B为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.小王同学测得∶洗手液瓶子的底面直径 , 喷嘴位置点B距台面的距离为 , 且三点共线.小王在距离台面处接洗手液时,手心Q到直线的水平距离为 , 若小王不去接,则洗手液落在台面的位置距的水平面是( )
A、 B、 C、 D、8. 学校组织学生去绍兴进行研学实践活动,小王同学发现在宾馆房间的洗手盘台面上有一瓶洗手液(如图①).于是好奇的小王同学进行了实地测量研究.当小王用一定的力按住顶部A下压如图②位置时,洗手液从喷口B流出,路线近似呈抛物线状,且喷口B为该抛物线的顶点.洗手液瓶子的截面图下面部分是矩形.小王同学测得∶洗手液瓶子的底面直径 , 喷嘴位置点B距台面的距离为 , 且三点共线.小王在距离台面处接洗手液时,手心Q到直线的水平距离为 , 若小王不去接,则洗手液落在台面的位置距的水平面是( )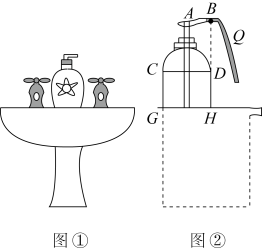 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
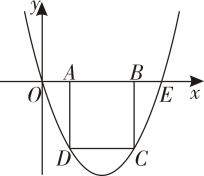
9. 如图,在平面直角坐标系中,抛物线与轴的正半轴交于点.矩形的边在线段上,点C、D在抛物线上,则矩形周长的最大值为.
 10. “地摊经济”一时兴起,小惠计划在夜市销售一款产品,进价每件40元,售价每件110元,每天可以销售20件,每销售一件需缴纳摊位管理费用a元(a>0).未来30天,这款产品将开展“每天降价1元”的大促销活动,即从第一 天起每天的单价均比前天降1元,通过市场调研发现:该产品单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳摊位管理费用后的利润随天数t ( t为正整数)的增大而增大,则a的取值范围应为.11. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
10. “地摊经济”一时兴起,小惠计划在夜市销售一款产品,进价每件40元,售价每件110元,每天可以销售20件,每销售一件需缴纳摊位管理费用a元(a>0).未来30天,这款产品将开展“每天降价1元”的大促销活动,即从第一 天起每天的单价均比前天降1元,通过市场调研发现:该产品单价每降1元,每天销量增加4件.在这30天内,要使每天缴纳摊位管理费用后的利润随天数t ( t为正整数)的增大而增大,则a的取值范围应为.11. 如图,抛物线 (m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.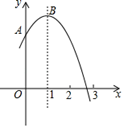
①抛物线 与直线y=m+2有且只有一个交点;
②若点 点 、点 在该函数图象上,则 ;
③将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为 ;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 ,其中正确判断的序号是
12. 已知抛物线 交x轴于点A,B (B在x轴正半轴上),交y轴于点C,△ABC是等腰三角形,则a的值为 .13. 如图所示,从高为2m的点 处向右上抛一个小球 ,小球路线呈抛物线 形状,小球水平经过2m时达到最大高度6m,然后落在下方台阶B处弹起,已知 m, m, m,若小球弹起形成一条与 形状相同的抛物线,且落点 与 , 在同一直线上,则小球弹起时的最大高度是m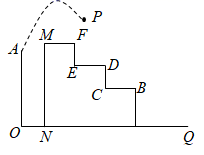
三、解答题
-
14. 排球考试要求:垫球后,球在运动中离地面的最大高度至少为2米.某次模拟测试中,某生第一次在处将球垫偏,之后又在A、两处先后垫球,球沿抛物线运动(假设抛物线、、在同一平面内),最终正好在处垫住,处离地面的距离为1米.如图所示,以为坐标原点1米为单位长度建立直角坐标系,轴平行于地面水平直线 , 已知点 , 点的横坐标为 , 抛物线表达式为和抛物线表达式为 .
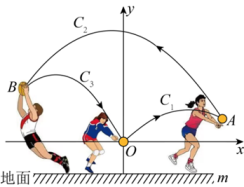 (1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?15. 李大爷每天到批发市场购进某种水果进行销售,这种水果每箱10千克,批发商规定:整箱购买,一箱起售,每人一天购买不超过10箱;当购买1箱时,批发价为8.2元/千克,每多购买1箱,批发价每千克降低0.2元.根据李大爷的销售经验,这种水果售价为12元/千克时,每天可销售1箱;售价每千克降低0.5元,每天可多销售1箱.(1)、请求出这种水果批发价(元/千克)与购进数量(箱)之间的函数关系式;(2)、若每天购进的这种水果需当天全部售完,请你计算,李大爷每天应购进这种水果多少箱,才能使每天所获利润最大?最大利润是多少?
(1)、求抛物线的函数表达式;(2)、第一次垫球后,球在运动中离地面的最大高度是否达到要求?请说明理由;(3)、为了使第三次垫球后,球在运动中离地面的最大高度达到要求,该生第三次垫球处离地面的高度至少为多少米?15. 李大爷每天到批发市场购进某种水果进行销售,这种水果每箱10千克,批发商规定:整箱购买,一箱起售,每人一天购买不超过10箱;当购买1箱时,批发价为8.2元/千克,每多购买1箱,批发价每千克降低0.2元.根据李大爷的销售经验,这种水果售价为12元/千克时,每天可销售1箱;售价每千克降低0.5元,每天可多销售1箱.(1)、请求出这种水果批发价(元/千克)与购进数量(箱)之间的函数关系式;(2)、若每天购进的这种水果需当天全部售完,请你计算,李大爷每天应购进这种水果多少箱,才能使每天所获利润最大?最大利润是多少?