人教版九年级上学期数学课时进阶测试22.3实际问题与二次函数（一阶）

试卷更新日期：2024-07-02 类型：同步测试

进入出卷网下载

一、选择题

1. 一件商品的原价是240元，经过两次降价后的价格为y元，若设两次的平均降价率为x ，则y与x的函数关系式是（）

A、 $y = 240 (1 - 2 x)$ B、 $y = 240 (1 + 2 x)$ C、 $y = 240 {(1 - x)}^{2}$ D、 $y = 240 {(1 + x)}^{2}$

查看试题解析
2. 某大桥的桥拱可以用抛物线的一部分表示，函数关系为 $y = - \frac{1}{25} x^{2}$ ，当水面宽度 $A B$ 为 $20 m$ 时，水面与桥拱顶的高度 $C O$ 等于（）

A、 $2 m$ B、 $4m$ C、 $10 m$ D、 $16m$

查看试题解析
3. 已知一个直角三角形两直角边长的和为10，设其中一条直角边长为x，则直角三角形的面积y与x之间的函数关系式是（）

A、y=- $\frac{1}{2}$ x²+5x B、y=-x²+10x C、y= $\frac{1}{2}$ x²+5x D、y=x²+10x

查看试题解析
4. 在一次炮弹发射演习中，记录到一门迫击炮发射的炮弹的飞行高度y米与飞行时间x秒的关系式为 $y = \frac{1}{5} x^{2} + 10 x$ ，当炮弹落到地面时，经过的时间为（）

A、40秒 B、45秒 C、50秒 D、55秒

查看试题解析
5. 已知实心球运动的高度y（m）与水平距离x（m）之间的函数关系是y＝-（x-1）²+4，则该同学此次投掷实心球的成绩是（）

A、2m B、3m C、3.5m D、4m

查看试题解析
6. 据省统计局公布的数据，合肥市2023年第一度GDP总值约为26千亿元人民币，若我市第三季度GDP总值为y千亿元人民币，平均每个季度GDP增长的百分率为x ，则y关于x的函数表达式是（）

A、 $y = 2.6 (1 + 2 x)$ B、 $y = 2.6 {(1 - x)}^{2}$ C、 $y = 2.6 {(1 + x)}^{2}$ D、 $y = 2.6 + 2.6 (1 + x) + 2.6 {(1 + x)}^{2}$

查看试题解析
7. 如图，铅球运动员掷铅球的高度y（m）与水平距离x（m）之间的函数解析式是 $y = - \frac{1}{12} x^{2} + \frac{2}{3} x + \frac{5}{3}$ ，则该运动员此次掷铅球的成绩是（）

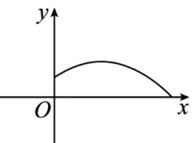A、6m B、12m C、8m D、10m

查看试题解析

二、填空题

8. 如图，一名学生推铅球，铅球行进高度y（单位：m）与水平距离x（单位：m）之间的关系是 $y = - \frac{1}{9} (x - 9) (x + 2)$ $，$ 则铅球被推出的水平距离 $O A$ 为 m．

查看试题解析
9. 从地面竖直向上抛出一小球，小球的高度 $h$ （米）与小球的运动时间（秒）之间的关系式是 $h = 30 t - 5 t^{2} (0 \leq t \leq 6)$ ，若抛出小球1秒钟后再抛出同样的第二个小球．则第二个小球抛出秒时，两个小球在空中的高度相同．

查看试题解析
10. 某超市一月份的营业额是200万元，一月、二月、三月的营业额共 $y$ 万元，如果平均每月增长率为 $x$ ，那么营业额 $y$ 关于月平均增长率 $x$ 的函数表达式为.

查看试题解析
11. 某件商品的销售利润y（元）与商品单价x（元）之间满足 $y = - x^{2} + 6 x - 7$ ，不考虑其他因素，该商品的单价定为元时，销售一件该商品获得的利润最大，最大利润为元．

查看试题解析
12. 用长12m的铝合金条制成矩形窗框（如图所示），那么这个窗户的最大透光面积是（中间横框所占的面积忽略不计）

查看试题解析

三、解答题

13. 赵州桥的桥拱是近似的抛物线形，建立下图所示的平面直角坐标系，当水面宽度AB为10m时，水面离桥拱顶的高度DO是1m．

(1)、求这个抛物线的函数表达式．

(2)、当水面再上升0.5m时，求水面宽度．

查看试题解析
14. 椒江某童装专卖店在销售中发现，一款童装每件进价为80元，销售价为120元时，每天可售出20件，为了迎接“十一”国庆节，商店决定采取适当的降价措施，以扩大销售量，增加利润，经市场调查发现，如果每件童装降价5元，那么平均可多售出10件．

(1)、设每件童装降价x元时，每天可销售件，每件盈利元；(用x的代数式表示)

(2)、每件童装降价多少元时，平均每天盈利1200元．

(3)、设专卖店每天销售这款童装可获利润W元，当x为多少时W最大，最大值是多少？

查看试题解析