人教版八年级上学期数学课时进阶测试12.1全等三角形（三阶）

试卷更新日期：2024-07-02 类型：同步测试

进入出卷网下载

一、选择题

1. 长为1的一根绳，恰好可围成两个全等三角形，则其中一个三角形的最长边x的取值范围为（　　）

A、 $\frac{l}{6} \leq x < \frac{l}{4}$ B、 $\frac{l}{8} \leq x < \frac{l}{4}$ C、 $\frac{l}{6} < x < \frac{l}{4}$ D、 $\frac{l}{8} < x < \frac{l}{4}$

查看试题解析
2. 如图，在平面直角坐标系中，点A、B的坐标分别是（﹣3，0），（0，6），若△AOB≌△CDA，则点D的坐标是（）

A、（﹣9，0） B、（﹣6，0） C、（0，﹣9） D、（﹣12，0）

查看试题解析
3. 如图， $△ A B C$ ≌ $△ D E C$ ，点 $A$ 和点 $D$ 是对应顶点，点 $B$ 和点 $E$ 是对应顶点，过点 $A$ 作 $A F ⊥ C D$ ，垂足为点 $F$ ，若 $∠ B C E = 65 °$ ，则 $∠ C A F$ 的度数为（）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $65 °$

查看试题解析
4. 边长都为整数的△ABC≌△DEF ，AB与DE是对应边，AB=2，BC=4，若△DEF的周长为偶数，则 DF的取值为（）

A、3 B、4 C、5 D、3或4或5

查看试题解析
5. 下列说法：①全等三角形的形状相同、大小相等，②三边对应相等的两个三角形全等，③全等三角形的对应角的平分线相等，④全等三角形的面积相等．

A、①②④ B、①③④ C、②③④ D、①②③④

查看试题解析
6. 如图，已知在正方形 $A B C D$ 中， $A B = B C = C D = A D = 10$ 厘米， $∠ A = ∠ B = ∠ C = ∠ D = 9 0^{°}$ ，点E在边 $A B$ 上，且 $A E = 4$ 厘米，如果点P在线段BC上以2厘米／秒的速度由B点向C点运动，同时，点Q在线段 $C D$ 上由C点向D点运动，设运动时间为t秒，当ΔBPE与ΔCQP全等时，t的值为（　　）

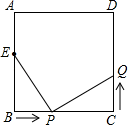A、2 B、2或1.5 C、2.5 D、2.5或2

查看试题解析
7. 如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形 $A B C D$ 、正方形 $E F G H$ 、正方形 $M N P Q$ 的面积分别为 $S_{1} ， S_{2} ， S_{3}$ ．若 $S_{1} + S_{2} + S_{3} = 60$ ，则 $S_{2}$ 的值是（）

A、30 B、20 C、18 D、10

查看试题解析

二、填空题

8. 三个全等三角形按如图的形式摆放，则 $∠ 1 + ∠ 2 + ∠ 3$ 的度数是.

查看试题解析
9. 如图，在平面直角坐标系中，矩形OABC的两边分别在x轴和y轴上，OA＝10cm，OC＝6cm，F是线段OA上的动点，从点O出发，以1cm/s的速度沿OA方向作匀速运动，点Q在线段AB上．已知A，Q两点间的距离是O，F两点间距离的a倍，若用（a，t）表示经过时间t（x）时，△OCF，△FAQ，△CBQ中有两个三角形全等，请写出（a，t）的所有可能情况．

查看试题解析
10. 在直角坐标系中，如图有△ABC，现另有一点D满足以A、B、D为顶点的三角形与△ABC全等，则D点坐标为

查看试题解析
11. 如图， $△ A B E ≌ △ A D C ≌ △ A B C$ ，若 $∠ 1 = 150 °$ ，则 $∠ α$ 的度数为．

查看试题解析

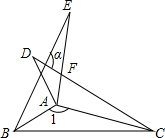
三、解答题

12. 如图，在平面直角坐标系中，O为坐标原点．A、B两点的坐标分别为 $A （ m,0）$ 、 $B （0, n ）$ ，且 $| m − n −3|+ \sqrt{2 n −6} =0$ ，点P从A出发，以每秒1个单位的速度沿射线 $A O$ 匀速运动，设点P运动时间为t秒．

(1)、求 $O A$ 、OB的长；

(2)、连接 $P B$ ，若 $△ P O B$ 的面积不大于3且不等于0，求t的范围；

(3)、过P作直线AB的垂线，垂足为D，直线 $P D$ 与y轴交于点E，在点P运动的过程中，是否存在这样的点P，使 $△ E O P ≌△ A O B$ ？若存在，请求出t的值；若不存在，请说明理由．

查看试题解析

四、综合题

13. 如图，在 $△ A B C$ 中， $B C = 8$ cm， $A G // B C$ ， $A G = 8$ cm，点F从点B出发，沿线段 $B C$ 以4cm/s的速度连续做往返运动，点E从点A出发沿线段 $A G$ 以2cm/s的速度运动至点G，E、F两点同时出发，当点E到达点G时，E、F两点同时停止运动， $E F$ 与 $A C$ 交于点D，设点E的运动时间为t（秒）

(1)、分别写出当 $0 < t < 2$ 和 $2 < t < 4$ 时线段 $B F$ 的长度（用含t的代数式表示）

(2)、当 $B F = A E$ 时，求t的值；

(3)、当 $△ A D E ≌ △ C D F$ 时，直接写出所有满足条件的 $t$ 值.

查看试题解析