浙教版数学八年级暑假知识训练：数据的初步分析

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 数据2、 $a$ 、3、4的平均数是3，则 $a$ 的值是 $($ $)$

A、1 B、2 C、3 D、4

查看试题解析
2. 在一次献爱心的捐款活动中，某班50名同学的捐款金额如图所示，则在这次捐款活动中，该班同学捐款金额的平均数是（）

A、14.2元 B、15元 C、16.2元 D、20.25元

查看试题解析
3. 已知一组数据1，2，3，5，5，6．则这组数据的中位数和众数分别是（）

A、3和5 B、4和5 C、5和5 D、5和6

查看试题解析
4. 为筹备班级联欢会，班长对全班同学喜爱的水果做了民意调查，最值得关注的统计量是（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
5. 在一次献爱心捐款活动中，五名同学捐款数（单位：元）分别是5，3，6，5，10，捐10元的同学后来又追加了 10元.追加后的5个数据与之前的5个数据相比，集中趋势相同的是（）

A、只有平均数 B、只有中位数 C、只有众数 D、中位数和众数

查看试题解析

二、填空题（每题4分，共24分）

6. 已知数据 $x_{1}, x_{2}, x_{3}$ 的平均数是2，数据 $x_{4}, x_{5}$ 的平均数是4，则 $x_{1}, x_{2}, x_{3}$ ， $x_{4}, x_{5}$ 这组数据的平均数是.

查看试题解析
7. 已知一组数据1，4，5，7， $x$ 的平均数为4，则这组数据的中位数为．

查看试题解析
8. 如图是容容前三次购买苹果单价的统计图，第四次又买的苹果单价是a元/千克，发现这四个单价的中位数恰好也是众数，则 $a =$ ．

查看试题解析
9. 一组数据1，3，2，2，a，b，c的唯一众数为3，平均数为2，则这组数据的方差为．

查看试题解析
10. 小明利用公式 $S_{}^{2} = \frac{1}{n} [{(1 - \bar{x})}_{}^{2} + {(2 - \bar{x})}_{}^{2} + {(3 - \bar{x})}_{}^{2} + {(4 - \bar{x})}_{}^{2} + {(5 - \bar{x})}_{}^{2}]$ 计算若干个数的方差，则这些数的标准差为 .

查看试题解析

三、解答题（共6题，共49分）

11. 解答下列各题：

(1)、用配方法解一元二次方程： $2 x^{2} + 4 x - 3 = 0$ ．

(2)、已知一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ ， $x_{4}$ 的平均数是5，求数据 $5 x_{1} - 5$ ， $5 x_{2} - 5$ ， $5 x_{3} - 5$ ， $5 x_{4} - 5$ 的平均数．

查看试题解析
12. 学校组织“四大名著”知识竞赛，每班派20名同学参加，成绩分为 $A$ ， $B$ ， $C$ ， $D$ 四个等级，其中相应等级的得分依次记为100分，90分，80分，70分．现将八年级1班和2班的成绩整理如下：

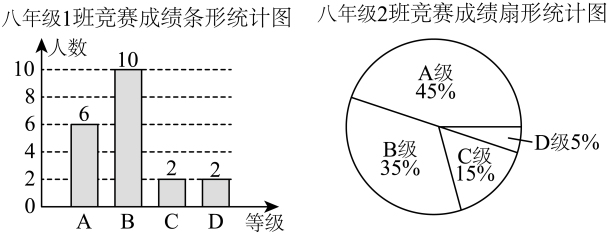(1)、填写表格；
班级
平均数
众数
中位数
八年级1班
分
90分
分
八年级2班
92分
分
90分

(2)、结合（1）中的统计量，你认为哪个班级的竞赛成绩更加优秀？请说明理由．

查看试题解析
13. 某校对九年级3个班级进行综合素质考评，下表是它们五项素质考评得分表（以分为单位，每项满分为10分）．
班级
行为规范
学习成绩
校运动会
艺术获奖
劳动卫生
九年级（1）班
10
10
6
10
7
九年级（5）班
10
8
8
9
8
九年级（8）班
9
10
9
6
9

(1)、计算各班五项考评分的平均数．

(2)、现要从三个班级中选送一个班级为市级先进班集体候选班，并设定如下规则：
行为规范：学习成绩：校运动会：艺术获奖：劳动卫生 $= 3 : 3 : 2 : 1 : 1$ ．请通过计算说明推荐市级先进班集体候选班是哪个班？

查看试题解析
14. 为庆祝中国共产主义青年团成立 100 周年，学校团委在八、九年级各抽取 50 名团员开展团知识竞赛，为便于统计成绩，制订了取整数的计分方式，满分 10 分．竞赛成绩如图所示：
项目
众数
中位数
方差
八年级竞赛成绩
7
8
1.88
九年级竞赛成绩
$a$
8
$b$

(1)、你能用成绩的平均数判断哪个年级的成绩比较好吗? 通过计算说明．

(2)、请根据图表中的信息，回答下列问题．
① 表中的 $a =$ ， $b =$ .
② 现要给成绩突出的年级颁奖，如果分别从众数和方差两个角度来分析，你认为应该给哪个年级颁奖?

查看试题解析
15. 某厂生产A，B两种产品，其单价随市场变化而做相应调整．营销人员根据前三次单价变化的情况，绘制了如下统计表及折线图（不完整），并求得了A产品三次单价的平均数和方差： ${\bar{x}}_{A} = 5.9, S_{A}^{2} = \frac{43}{150}$ ．
A，B产品单价变化统计表

第一次
第二次
第三次
A产品单价（元/件）
6
5.2
6.5
B产品单价（元/件）
3.5
4
3

(1)、补全图中B产品的单价变化折线图．B产品第三次的单价比上一次的单价降低了%．

(2)、求B产品三次单价的方差，并比较哪种产品的单价波动较小．

(3)、该厂决定第四次调价，A产品的单价仍为6.5元/件，B产品的单价比3元/件上调m%（m>0），但调价后不能超过4元/件，并且使得A产品这四次单价的中位数是B产品四次单价中位数的2倍少1．求m的值．

查看试题解析

16. 称五筐大白菜的重量，得到如下统计表中甲组数据．把甲组数据的每个数都减去

40

，得到统计表中的乙组数据，将这两组数据分别画成折线统计图（未完成．单位：千克）．

甲组、乙组数据统计表

序号	1	2	3	4	5
甲组数据	$38$	$42$	$38$	$39$	$43$
乙组数据	$- 2$	2	$- 2$	$- 1$	3

请完成下列问题：

(1)、完成乙组数据的折线统计图．

(2)、①分别求出甲、乙两组数据的平均数

\bar{x_{甲}}

，

\bar{x_{乙}}

，并直接写出

\bar{x_{甲}}

与

\bar{x_{乙}}

之间满足的数量关系式．

②甲、乙两组数据的方差分别为 ${S^{2}}_{甲}$ ， ${S^{2}}_{乙}$ ，请比较 ${S^{2}}_{甲}$ ， ${S^{2}}_{乙}$ 的大小，并说明理由．

查看试题解析

四、实践探究题（共2题，共17分）

17. 某班开展一次综合与实践活动，部分记载如下：
【活动主题】利用树叶的特征对树木进行分类．
【实践过程】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如表：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【问题解决】

(1)、同学们通过计算得到芒果树叶的长宽比的平均数是3.74，请你继续计算出荔枝树叶的长宽比的平均数；

(2)、从树叶的长宽比的平均数来看，现有一片长13cm，宽6.5cm的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

查看试题解析
18. 综合与实践
【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：

1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：

平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
2.0
n
0.0669
问题解决】

(1)、上述表格中， $m =$ ， $n =$ ；

(2)、①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大．”
②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍．”
上面两位同学的说法中，合理的是（填序号）

(3)、现有一片长 $11 c m$ ，宽 $5.6 c m$ 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由．

查看试题解析

班级	平均数	众数	中位数
八年级1班	分	90分	分
八年级2班	92分	分	90分

班级	行为规范	学习成绩	校运动会	艺术获奖	劳动卫生
九年级（1）班	10	10	6	10	7
九年级（5）班	10	8	8	9	8
九年级（8）班	9	10	9	6	9

项目	众数	中位数	方差
八年级竞赛成绩	7	8	1.88
九年级竞赛成绩	$a$	8	$b$

	第一次	第二次	第三次
A产品单价（元/件）	6	5.2	6.5
B产品单价（元/件）	3.5	4	3

	1	2	3	4	5	6	7	8	9	10
芒果树叶的长宽比	3.8	3.7	3.5	3.4	3.8	4.0	3.6	4.0	3.6	4.0
荔枝树叶的长宽比	2.0	2.0	2.0	2.4	1.8	1.9	1.8	2.0	1.3	1.9