浙教版数学八年级暑假知识训练:弧长与扇形的面积
试卷更新日期:2024-06-30 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 已知扇形的圆心角为 , 半径为 , 则弧长为( )A、 B、 C、 D、2. 若一个扇形的半径为6,圆心角为120°,则该扇形的面积是( )A、2π B、4π C、12π D、24π3. 计算半径为1,圆心角为的扇形面积为( )A、 B、 C、 D、4. 如图,AB是 的直径,弦 , , ,则阴影部分的面积为( )
 A、 B、 C、 D、5. 如图所示的网格中,每个小正方形的边长均为1,点A , B , D均在小正方形的顶点上,且点B , C在弧上, , 则的长为( )
A、 B、 C、 D、5. 如图所示的网格中,每个小正方形的边长均为1,点A , B , D均在小正方形的顶点上,且点B , C在弧上, , 则的长为( ) A、 B、 C、 D、6. 如图所示,正六边形ABCDE的边长为6,以顶点为圆心、AB的长为半径画圆,则图中阴影部分的面积为( ).
A、 B、 C、 D、6. 如图所示,正六边形ABCDE的边长为6,以顶点为圆心、AB的长为半径画圆,则图中阴影部分的面积为( ). A、 B、 C、 D、7. 如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )
A、 B、 C、 D、7. 如图,用一个半径为5 cm的定滑轮带动重物上升,滑轮上一点P旋转了108°,假设绳索(粗细不计)与滑轮之间没有滑动,则重物上升了( )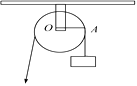 A、π cm B、2π cm C、3π cm D、5π cm8. 如图所示,王虎使一长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )
A、π cm B、2π cm C、3π cm D、5π cm8. 如图所示,王虎使一长为4 cm,宽为3 cm的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为A→A1→A2 , 其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为( )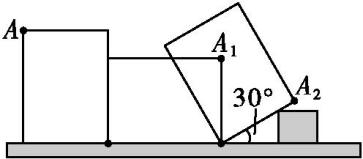 A、10 cm B、4π cm C、π cm D、 cm9. 如图所示,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊A(羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米.
A、10 cm B、4π cm C、π cm D、 cm9. 如图所示,一根5米长的绳子,一端拴在围墙墙角的柱子上,另一端拴着一只羊A(羊在草地上活动),那么羊在草地上的最大活动区域面积是( )平方米. A、 B、 C、 D、10. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )
A、 B、 C、 D、10. 习近平总书记强调:“青年一代有理想、有本领、有担当,国家就有前途,民族就有希望”.如图①是一块弘扬“新时代青年励志奋斗”的扇面宣传展板,该展板的部分示意图如图②所示,它是以O为圆心, , 长分别为半径,圆心角形成的扇面,若 , , 则阴影部分的面积为( )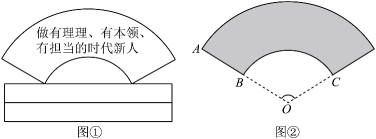 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
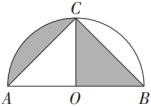
11. 用一个圆心角为120°,半径为的扇形制作一个圆锥的侧面,这个圆锥的底面半径为cm.12. 如图,以点O为圆心,AB为直径的半圆过点C , 若C为的中点, , 则阴影部分的面积是 .
 13. 已知扇形面积为 , 半径为 , 则扇形的弧长为 .14. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .
13. 已知扇形面积为 , 半径为 , 则扇形的弧长为 .14. 如图Rt△ABC,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”:当AC=6,BC=8时,则阴影部分的面积为 .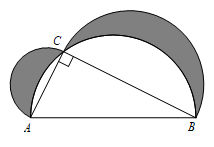 15. 如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为160°的圆弧形窗帘轨道(如图2)需用此材料mm,则此圆弧所在圆的半径为mm.
15. 如图1所示的铝合金窗帘轨道可以直接弯曲制作成弧形.若制作一个圆心角为160°的圆弧形窗帘轨道(如图2)需用此材料mm,则此圆弧所在圆的半径为mm. 16. 如图是明清时期女子主要裙式之一的马面裙,图马面裙可以近似地看作扇环,其中的长度为米,的长度为米,圆心角 , 则裙长为 米
16. 如图是明清时期女子主要裙式之一的马面裙,图马面裙可以近似地看作扇环,其中的长度为米,的长度为米,圆心角 , 则裙长为 米
三、解答题(共7题,共66分)
-
17. 如图,在平面角坐标系中,已知的三个顶点坐标分别为 , , , 将绕原点O顺时针旋转90°后得到 .
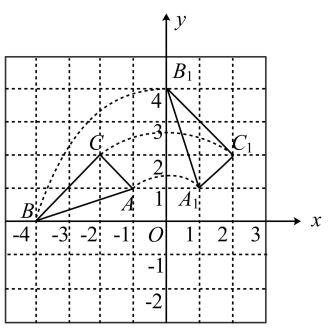 (1)、请写出、、三点的坐标:
(1)、请写出、、三点的坐标:, , ;
(2)、求点B旋转到点的弧长.18. 如图,在平面直角坐标系中,△OAB的三个顶点的坐标分别为O(0,0)A(5,3),B(0,5).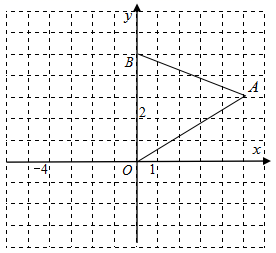 (1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.19. 如图,以的一边为直径作交于点 , , 与边的交点恰好为的中点 , 连结 .
(1)、画出△OAB绕原点O逆时针方向旋转90°后得到的△OA1B1;(2)、∠OAA1=;(3)、求旋转过程中,线段OB扫过的图形的面积.19. 如图,以的一边为直径作交于点 , , 与边的交点恰好为的中点 , 连结 . (1)、求证: .(2)、若 , 求弧的长.20. 如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接.
(1)、求证: .(2)、若 , 求弧的长.20. 如图,内接于⊙O,交⊙O于点D,交于点E,交⊙O于点F,连接. (1)、求证:;(2)、若⊙O的半径为3, , 求的长(结果保留π).21. 如图,是⊙O的直径,点A在⊙O上且平分弧 , 于点 , 分别交 , 于 , .
(1)、求证:;(2)、若⊙O的半径为3, , 求的长(结果保留π).21. 如图,是⊙O的直径,点A在⊙O上且平分弧 , 于点 , 分别交 , 于 , . (1)、求证:;(2)、若 , 求阴影部分面积.
(1)、求证:;(2)、若 , 求阴影部分面积.