浙教版数学八年级暑假知识训练：正多边形

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 正十二边形的一个外角的度数为（）

A、30° B、36° C、144° D、150°

查看试题解析
2. 已知正多边形的一个外角等于45°，那么这个正多边形的边数为（）

A、6 B、7 C、8 D、9

查看试题解析
3. 一个圆的内接正多边形中，一条边所对的圆心角为72°，则该正多边形的边数是（）

A、4 B、5 C、6 D、7

查看试题解析
4. 一个半径为2cm的圆的内接正六边形的面积是（　　）

A、24cm² B、6 $\sqrt{3}$ cm² C、12 $\sqrt{3}$ cm² D、8 $\sqrt{3}$ cm²

查看试题解析
5. 正十边形的每个内角都是（）

A、 $36 °$ B、 $72 °$ C、 $108 °$ D、 $144 °$

查看试题解析
6. 边长为6的正三角形的外接圆的半径为（）

A、2 $\sqrt{3}$ B、 $\sqrt{3}$ C、 $\sqrt{3}$ π D、2 $\sqrt{3}$ π

查看试题解析
7. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，正六边形的周长是12，则 $⊙ O$ 的半径是（）

A、1 B、 $\sqrt{3}$ C、2 D、 $2 \sqrt{3}$

查看试题解析
8. 利用圆的等分，在半径为 $2 \sqrt{3}$ 的圆中作出六芒星图案，则图中阴影部分的面积为（）

A、6 B、 $6 \sqrt{3}$ C、12 D、 $12 \sqrt{3}$

查看试题解析
9. 如图，正六边形 $A B C D E F$ 内接于 $⊙ O$ ，若 $⊙ O$ 的周长是 $12 π$ ，则正六边形的边长是（）

A、 $2 \sqrt{3}$ B、3 C、6 D、 $3 \sqrt{3}$

查看试题解析
10. 作⊙O的内接正六边形ABCDEF ，甲、乙两人的作法分别是：
甲：第一步：在⊙O上任取一点A ，从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B ， C ， D ， E ， F ．第二步：依次连接这六个点．
乙：第一步：任作一直径AD ．第二步：分别作OA ， OD的中垂线与⊙O相交，交点从点A开始，依次为点B ， C ， E ， F ．第三步：依次连接这六个点．
对于甲、乙两人的作法，可判断（）

A、甲正确，乙错误 B、甲、乙均错误 C、甲错误，乙正确 D、甲、乙均正确

查看试题解析

二、填空题（每题4分，共24分）

11. 已知正n边形的每一个内角都等于144°，则n的值为.

查看试题解析
12.

(1)、已知正多边形的一个内角为135°，则该正多边形是正边形．

(2)、已知一个正多边形的每个外角都等于36°，那么它是正边形．

查看试题解析
13. 若一个正多边形的每个内角为150°，则这个正多边形的边数是．

查看试题解析
14. 如图，正五边形ABCDE内接于⊙O，则∠ABD＝．

查看试题解析
15. 如图，在正六边形ABCDEF中，以点A为原点建立直角坐标系，边AB落在x轴上．若点B的坐标为(2，0)，则点C的坐标是．

查看试题解析
16. 刘徽是我国魏晋时期卓越的数学家，他首次提出“割圆术”，利用圆内接正多边形逐步逼近圆来近似计算圆周率，方法如图：作正六边形ABCDEF内接于 $⊙ O$ ，取 $\overset{⌢}{A B}$ 的中点G， $O G$ 与 $A B$ 交于点H；连接 $A G$ 、 $B G$ ；依次对剩余五段弧取中点可得一个圆内接正十二边形，记正十二边形的面积为 $S_{1}$ ，正六边形的面积为 $S_{2}$ ，则 $\frac{S_{1}}{S_{2}} =$ .

查看试题解析

三、解答题（共8题，共66分）

17.
如图，以正六边形ABCDEF的边AB为边，在形内作正方形ABMN，连接MC．求∠BCM的大小．

查看试题解析
18. 如图，正八边形 $A B C D E F G H$ 内接于 $⊙ O$ ， M是弧DE上的一点，连接AM ， BM ，求 $∠ A M B$ 的度数．

查看试题解析
19. 已知：如图，在圆内接正五边形ABCDE中，对角线AC，BD交于点P．

(1)、求∠APD的度数．

(2)、求证：四边形EAPD是菱形．

查看试题解析
20. 已知：如图，正六边形ABCDEF的边长为6cm，延长FE，CD，相交于点G．

(1)、求证：△FCG是正三角形．

(2)、求正三角形FCG的高线长．

查看试题解析
21. 如图，正方形ABCD的外接圆为⊙O，点P在劣弧 CD上（不与C点重合）．

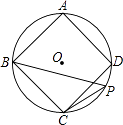(1)、求∠BPC的度数；

(2)、若⊙O的半径为8，求正方形ABCD的边长．

查看试题解析
22. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切（我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形）．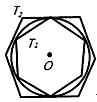

(1)、设T₁ ， T₂的边长分别为a，b，圆O的半径为r，求r：a及r：b的值；

(2)、求正六边形T₁ ， T₂的面积比S₁：S₂的值．

查看试题解析
23. 某数学学习小组的成员在探索“各内角都相等的圆内接多边形是否为正多边形”时，进行了如下探讨：
甲同学：我发现这种多边形不一定是正多边形.如圆内接矩形不一定是正方形.
乙同学：但是边数为3时，它是正三角形，而且我猜想，边数为5时，它应该是正五边形……
丙同学：我发现边数为6时，它也不一定是正六边形.如图甲所示， $△ A B C$ 是正三角形， $\overset{⌢}{A D} ， \overset{⌢}{B E} ， \overset{⌢}{C F}$ 均相等，很显然由此构造的六边形ADBECF并不是正六边形.

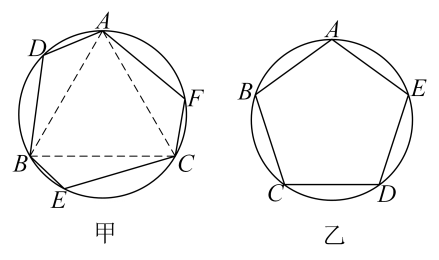(1)、如图乙所示，若圆内接五边形ABCDE的各内角均相等，则∠ABC= .请简要说明圆内接五边形ABCDE为正五边形的理由.

(2)、请证明丙同学构造的六边形各内角相等.

(3)、根据以上的探索过程，就“各内角都相等的圆内接多边形是否为正多边形”的结论与“边数n(n≥3，n为整数)”的关系，请提出你的猜想.(不需证明)

查看试题解析