浙教版数学八年级暑假知识训练：圆内四边形

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 如图，四边形ABCD内接于⊙O ，若∠B＝108°，则∠D的度数为（）

A、34° B、42° C、54° D、72°

查看试题解析
2. 四边形ABCD内接于⊙O，若∠ADC=80°，则∠ABC的度数是（）

A、40° B、80° C、120° D、100°

查看试题解析
3. 四边形ABCD内接于 $⊙ O$ ， $∠ B = 100 °$ ，则 $∠ D$ 的度数是（）

A、 $60 °$ B、 $80 °$ C、 $100 °$ D、 $120 °$

查看试题解析
4. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AED＝20°，则∠BCD的度数为(　　)

A、100° B、110° C、115° D、120°

查看试题解析
5. 如图，已知四边形ABCD内接于⊙O，若∠ADC＝110°，则∠AOC等于（）°.

A、130 B、140 C、150 D、160

查看试题解析
6. 如图，点A ， B ， C ， D ， E均在 $⊙ O$ 上，且 $B D$ 经过圆心O ，连接 $A B ， A E ， C E$ ，若 $∠ B + ∠ E = 150 °$ ，则弧 $C D$ 所对的圆心角的度数为（）

A、 $30 °$ B、 $40 °$ C、 $50 °$ D、 $60 °$

查看试题解析
7. 如图，点C、D、E、F、G在以AB为直径的⊙O上，∠AGC＝20°，∠BFE＝10°，则∠CDE＝（）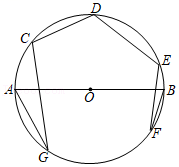

A、115° B、120° C、135° D、150°

查看试题解析
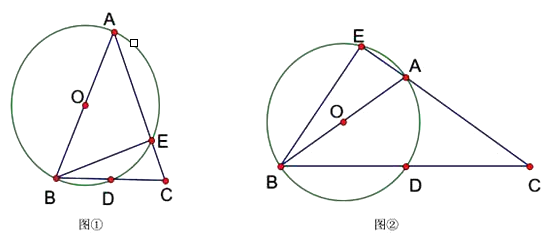
8. 如图，四边形ABCD是⊙O的内接四边形．若∠A：∠B：∠D=4：3：3，则∠DCE的度数是（）

A、100°． B、105°． C、110°． D、120°．

查看试题解析
9. 如图，半径为5的圆中有一个内接矩形 $A B C D ， A B > B C$ ，点 $M$ 是 $\overset{⌢}{A B C}$ 的中点， $M N ⊥ A B$ 于点 $N$ ，若矩形ABCD的面积为30，则线段MN的长为（）.

A、 $\sqrt{10}$ B、 $\frac{5}{2} \sqrt{2}$ C、 $\frac{\sqrt{70}}{2}$ D、 $2 \sqrt{10}$

查看试题解析
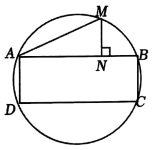10. 阿基米德折弦定理：如图1，AB与BC是⊙O的两条弦（即折线ABC是圆的一条折弦），AB＞BC，点M是 $\hat{A B C}$ 的中点，MN⊥AB于点N，则点N是折弦ABC的中点，即AN＝BN+BC．如图2，半径为4的圆中有一个内接矩形ABCD， AB＞BC，点M是 $\hat{A B C}$ 的中点， MN⊥AB于点N，若矩形ABCD的面积为20，则线段BN的长为（）

A、 $\sqrt{6}$ B、 $2 \sqrt{2}$ C、 $\sqrt{26} - \sqrt{6}$ D、 $\frac{5}{2}$

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，四边形ABCD是菱形，⊙O经过点A、C、D，与BC相交于点E，连接AC、AE.若∠D＝70°，则∠EAC的度数为.

查看试题解析
12. 如图，四边形 $A B C D$ 是 $⊙ O$ 的内接四边形， $∠ C B E$ 是它的一个外角，若 $∠ C B E = 100 °$ ，则 $∠ D$ 的度数是．

查看试题解析
13. 如图，AB是半圆O的直径，∠ABC＝40°，则∠D＝.

查看试题解析
14. 如图，四边形 $A B C O$ 的顶点 $A$ 、 $B$ 、 $C$ 在 $⊙ O$ 上，若 $∠ A B C = 130 °$ ，则 $∠ A O C =$ .

查看试题解析
15. 如图，点A，B，C，D，E都是⊙O上的点，AC=AE，∠D=128°，则∠B=°。

查看试题解析
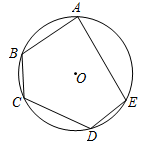16. 如图，四边形ABCD内接于⊙O，点M在AD的延长线上，∠AOC=142°，则∠CDM=.

查看试题解析

三、解答题（共6题，共60分）

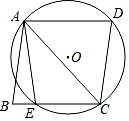
17. 如图，AB，AC是⊙O的两条弦，且AB=AC，D是 $\overset{⌢}{B C}$ 上一点，P是AC上一点．若∠BDC=150°，求∠APC的度数．

查看试题解析
18. 已知：如图，四边形ABCD内接于0O，延长DC，AB，交于点E，且BE=BC．
求证：△ADE是等腰三角形．

查看试题解析
19. 如图，四边形ABCD内接于⊙O，分别延长BC，AD，使它们相交于点E， $A B = 8$ ，且 $D C = D E$

(1)、求证： $∠ A = ∠ A E B .$

(2)、若 $∠ E D C = 9 0^{\circ}$ ，点C为BE的中点，求⊙O的半径．

查看试题解析
20. 如图，已知三角形 $Δ A B C$ 中，AB=AC，D是 $Δ A B C$ 的外接圆劣弧AC上的点（不与点A，C重合），延长BD至E。

(1)、求证：AD的延长线平分 $∠ C D E$

(2)、若 $∠ B A C = 3 0^{∘}$ ， $Δ A B C$ 中BC边上的高为 $2 + \sqrt{3}$ ，求外接圆的面积

查看试题解析
21. 如图，已知△ABC是⊙O的内接三角形，点P是 $\overset{⌢}{A B C}$ 的中点，过点P作PD⊥AB，交AB延长线于点D，连接BP．

(1)、求证：∠CBP＝∠PBD；

(2)、过P作PG⊥BC交BC于G点，若AB＝6，BD＝4，求BC的长．

查看试题解析
22. 已知△ABC中，AB=AC，以AB为直径的⊙O交BC于点D，交AC于点E．

(1)、当∠BAC为锐角时，如图①，求证：∠CBE= $\frac{1}{2} ∠ B A C$

(2)、当∠BAC为钝角时，如图②，CA的延长线与⊙O相交于点E，(1)中的结论是否仍然成立？并说明理由．

查看试题解析