浙教版数学八年级暑假知识训练：圆心角和圆周角
试卷更新日期：2024-06-30 类型：复习试卷
一、选择题（每题3分，共30分）
-
1. 下列说法中，正确的是（ ）A、同心圆的周长相等 B、面积相等的圆是等圆 C、相等的圆心角所对的弧相等 D、平分弧的弦一定经过圆心2. 下列说法正确的是（ ）A、长度相等的弧是等弧 B、相等的圆心角所对的弧相等 C、劣弧一定比优弧短 D、圆是轴对称图形，任何一条直径所在直线都是圆的对称轴3. 如图，OA，OC是⊙O的半径，点B在⊙O上，若AB∥OC，∠BCO=21°，则∠AOC的度数是（ ）
A、42° B、21° C、84° D、60°4. 如图，点在上， ， 则的度数是（ ）
A、 B、 C、 D、5. 如图，是的直径，点D，C在上，连接 ， ， ， 如果 ， 那么的度数是（ ）
A、15° B、20° C、25° D、30°6. 如图所示，是的直径， ， ， 则的度数为（ ）
A、 B、 C、 D、7. 如图，在⊙O中，∠A＝30°，劣弧的度数是（ ）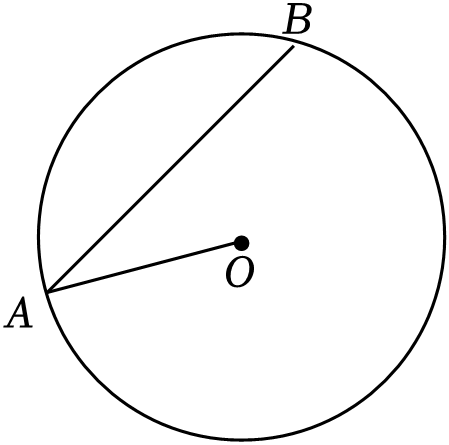
A、30° B、60° C、90° D、120°8. 如图，已知⊙O的半径为4，M是⊙O内一点，且OM＝2，则过点M的所有弦中，弦长是整数的共有（ ）
A、1条 B、2条 C、3条 D、4条9. 如图， 内接于⊙O，∠A＝74°，则∠OBC等于（ ）
A、17° B、16° C、15° D、14°10. 如图，△ABC内接于⊙O，DE，FG是⊙O的弦，AB＝DE，FG＝AC．下列结论：①DE+FG＝BC；②+＝；③∠DOE+∠FOG＝∠BOC；④∠DEO+∠FGO＝∠BAC．其中所有正确结论的序号是（ ）
A、①②③④ B、②③ C、②④ D、②③④二、填空题（每空2分，共26分）
-
11. 圆心角的度数和它所对的弧的度数12. 由圆的旋转不变性，得到圆心角定理：在中，相等的圆心角所对的相等，所对的也相等，并且这两条弦的弦心距也相等．13. 在同圆或等圆中，如果 ， ， ， 中有一对量相等，那么它们所对应的其余各对量都相等.14. 可以用圆的旋转不变性来理解圆心角定理及圆心角、弧、弦、弦心距这四个量之间的对应关系，要注意的是同一条弦对应条弧．15. 我们把1°的圆心角所对的弧叫做1°的弧.这样，n°的圆心角所对的弧就是.16. 同一圆中，一条弧所对的圆心角和圆周角分别为和90°，则.17. 直径为20cm的⊙O中，弦AB＝10cm ， 则弦AB所对的圆心角是 ．18. 如图，A、B、D是⊙O上三点，若∠A= 30°，则∠BOD =
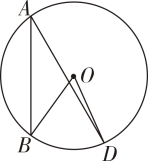
三、解答题（共7题，共64分）
-
19. 已知：如图，AB是⊙O的直径，弦AC与半径OD平行．
求证： ．
20. 已知，如图，AD=BC.求证：AB=CD
. 21. 如图， 的半径为2，四边形 内接于 ，圆心 到 的距离等于 .
(1)、求 的长；(2)、求 的度数.22. 已知：如图，在⊙O中，AB＝CD，AB与CD相交于点M，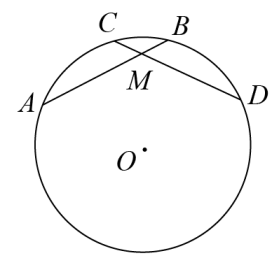
(1)、求证：；(2)、求证：AM＝DM．23. 如图，AB是⊙O的直径，C是的中点，CE⊥AB于点E，BD交CE于点F．
(1)、 求证：CF=BF．(2)、若CD=6，AC=8，求⊙O的半径及CE的长．24. 老师给小明出了一道题，小明感到有困难，请你帮助小明解决这个问题，题目是这样的：一个三角形两边长分别是3和4，第三边长是的一个实数根，请结合作图求这个三角形的外接圆面积．25. 在证明圆周角定理时，小岩所在的学习小组讨论出圆心与圆周角有三种不同的位置关系（如图1，2，3所示），并完成了情况一的证明．请你选择情况二或者情况三中的一种，完成证明．圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．
已知：中，所对的圆周角为 ， 圆心角为 ．
求证： ．
证明：
情况一（如图1）：
点在的一边上．
．
，
．
即 ．
情况二（如图2）：
点在的内部．
情况三（如图3）：
点在的外部．
