浙教版数学八年级暑假知识训练：垂径定理
试卷更新日期：2024-06-30 类型：复习试卷
一、选择题（每题3分，共30分）
-
1. 如图，的半径为5，弦 ， 点C在弦AB上，延长CO交于点D，则CD的取值范围是（ ）
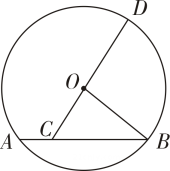A、 B、 C、 D、2. ⊙O的半径为5，M是圆外一点，MO＝6，∠OMA＝30°，则弦AB的长为（ ）
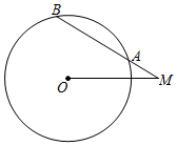A、4 B、6 C、6 D、83.如图，AB是⊙O的弦，OC⊥AB于点C，若AB=4，OC=1，则⊙O的半径为（ ）
A、 B、 C、2 D、64. 往直径为 的圆柱形容器内装入一些水以后，截面如图所示，若水面宽 ，则水的最大深度为（ ）
A、 B、 C、 D、5. 如图是雨水管示意图，截面是半径为50cm的圆，管内水面AB=80cm，则水深CD等于（ ）(单位：cm)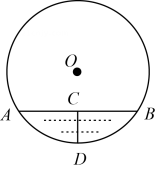
A、10 B、10 C、20 D、306. 如图，已知⊙O的直径CD=8，AB是⊙O的弦，AB⊥CD ， 垂足为M ， OM=2，则AB的长为（ ）
A、2 B、 C、4 D、7. 如图， ， ， ， ， 以点C为圆心，为半径的圆与、分别交于点E与点D ， 则的长为（ ）
A、 B、 C、 D、8. 如图，在⊙O中，AB是⊙O的弦，C为的中点，OC与AB交于点D，若⊙O的半径是10，CD=4，则AB=（ ）
A、14 B、15 C、17 D、169. 筒车是我国古代发明的一种水利灌溉工具，明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理，如图1．筒车盛水桶的运行轨道是以轴心O为圆心的圆，如图2．已知圆心O在水面上方，且⊙O被水面截得的弦AB长为6米，⊙O半径长为4米．若点C为运行轨道的最低点，则点C到弦AB所在直线的距离是（ ）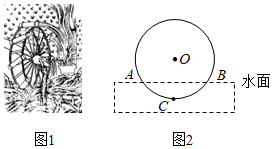
A、1米 B、（4﹣ ）米 C、2米 D、（4+ ）米10. 一次综合实践主题为：只用一张矩形纸条和刻度尺，如何测量一次性纸杯杯口的直径？小聪同学所在的学习小组想到了如下方法：如图，将纸条拉直并紧贴杯口，纸条的上下边沿分别与杯口相交于A，B，C，D四点，然后利用刻度尺量得该纸条的宽为4.25cm，AB＝2.5cm，CD＝6cm．请你帮忙计算纸杯的直径为（ ）
A、6cm B、cm C、7cm D、cm二、填空题（每空3分，共24分)
-
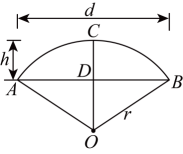
11. 如图，我国古代建造的闻名中外的赵州石拱桥，若桥拱圆弧的半径长为 ， 拱高为 ， 则桥跨度为（用含r、h的代数式表示）
12. 如图，PA交⊙O于点B，PB=4，AB=4，⊙O的半径为5，则OP的长为 ．
13. 已知⊙O的直径CD=10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB=8cm，则AC的长为 ．
14. 如图，△ABC是⊙O的内接等腰三角形，∠ABC=30°，弦EF过AB边的中点D ， 且EF∥BC ， 若BC＝ ， 则外接圆的半径为 ， EF=.
15. 如图，以矩形ABCD的边AB为直径作⊙O交另一边CD于点F，E，已知AB＝10，EF＝6，那么AD＝ ．
16. 图1是某游乐园的摩天轮，A，B两位同学坐在摩天轮上的示意图如图2，摩天轮半径OA为9米，两同学的直线距离AB为6米，当两位同学旋转到同一高度时（A在B的右侧），A同学距离地面的高度为 米，当A同学旋转到最高位置，此时两位同学的高度差为 米．
三、作图题(共8分）
-
17. 如图所示，破残的圆形轮片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D．AB=24cm，CD=8cm．
(1)、求作此残片所在的圆（不写作法，保留作图痕迹）；(2)、求（1）中所作圆的半径．四、解答题（共5题，共46分）
-
18. 如图，OA=OB，AB交⊙O于点C，D，OE是半径，且OE⊥AB于点F．
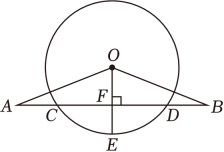(1)、求证：AC＝BD ．(2)、若CD＝4，EF＝1，求⊙O的半径．19. 如图，AB是⊙O的直径，弦AC= ， D是的中点，且CD∥AB．求CD的长．
20. 《九章算术》是我国古代数学成就的杰出代表作，书中记载：“今有中，不知大小．以锯锯之，深1寸，锯道长1尺，问经几何？“其意思为：“如图，今有一圆形木材在墙中，不知其大小用锯子去锯这个木材，锯口深DE＝1寸，锯道长AB＝10寸，问这块圆形木材的直径是多少？”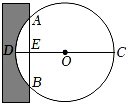
21. 如图，在半径为5的扇形AOB中，∠AOB＝90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．
(1)、当BC＝6时，求线段OD的长；(2)、在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度；如果不存在，请说明理由．22. 如图，某公路上有一隧道，顶部是圆弧形拱顶，圆心为O ， 隧道的水平宽AB为24m ， AB离地面的高度AE＝10m ， 拱顶最高处C离地面的高度CD为18m.若在拱顶的M ， N处安装照明灯，且M ， N离地面的高度相等，都为17m.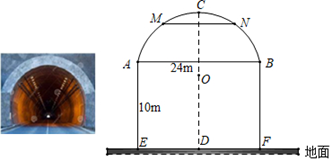
(1)、求圆弧形拱顶的半径的长度.(2)、求MN的长度.五、实践探究题
-
23.
测算石拱桥拱圈的半径
素材1
在日常生活中，如果没有带测量工具，那么我们可以用身体的“尺子”来测量，比如前臂长(包括手掌、手指)称为1肘(如图1)，现利用该方法测得一块矩形花岗岩的长和高(如图2)．
素材2
某数学兴趣小组测算一座石拱桥拱圈的半径(如图3)，石拱桥由以上矩形的花岗岩叠砌而成，上、下的花岗岩错缝连结(花岗岩的各个顶点落在上、下花岗各边的中点，如图3所示).
素材3
通过观察发现A，B两个点都在拱圈上.A是拱圈的最高点，且在两块花岗岩连结顶点处，B是花岗岩的顶点(如图4).
问题解决
任务1
获取数据
通过观察、计算A，B两点之间的水平距离及铅垂距离(高度差).
任务2
分析计算
通过观察、计算石拱桥拱圈的半径.
注：测量、计算时，都以“肘”为单位.
-