浙教版数学八年级暑假知识训练:图形的旋转
试卷更新日期:2024-06-30 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 以下生活现象中,属于旋转变换得是( )A、钟表的指针和钟摆的运动 B、站在电梯上的人的运动 C、坐在火车上睡觉 D、地下水位线逐年下降2. 如图,将绕点顺时针方向旋转到的位置,使得点 , 在同一条直线上, , 那么旋转角等于( )
 A、 B、 C、 D、3. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( )
A、 B、 C、 D、3. 图中的五角星图案,绕着它的中心旋转后,能与自身重合,则的值至少是( ) A、144 B、120 C、72 D、604. 如图,将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′,此点A在边B′C上,若BC=5,AC=3,则AB′的长为( )
A、144 B、120 C、72 D、604. 如图,将△ABC绕点C逆时针旋转一定的角度得到△A′B′C′,此点A在边B′C上,若BC=5,AC=3,则AB′的长为( ) A、5 B、4 C、3 D、25. 如图,在中, , 将绕点A逆时针旋转,点B落在点D处,则B、D两点间的距离为( )
A、5 B、4 C、3 D、25. 如图,在中, , 将绕点A逆时针旋转,点B落在点D处,则B、D两点间的距离为( ) A、 B、 C、3 D、6. 如图,教室里的水平地面有一个倒地的灰斗,与地面的夹角为 , , 小明同学将它扶起(将灰斗绕点C逆时针旋转)后平放在地面上,的对应线段为 , 在这一过程当中,灰斗柄绕点C旋转了( )
A、 B、 C、3 D、6. 如图,教室里的水平地面有一个倒地的灰斗,与地面的夹角为 , , 小明同学将它扶起(将灰斗绕点C逆时针旋转)后平放在地面上,的对应线段为 , 在这一过程当中,灰斗柄绕点C旋转了( ) A、 B、 C、 D、7. 小明将图
A、 B、 C、 D、7. 小明将图 案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( )
案绕某点连续旋转若干次,每次旋转相同角度 , 设计出一个外轮廓为正六边形的图案(如图),则可以为( ) A、30° B、60° C、90° D、120°8. 如图,在中, , 将绕点按逆时针方向旋转得到 . 若点刚好落在边上,且 , 则的度数为( )
A、30° B、60° C、90° D、120°8. 如图,在中, , 将绕点按逆时针方向旋转得到 . 若点刚好落在边上,且 , 则的度数为( ) A、 B、 C、 D、9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( )
A、 B、 C、 D、9. 在如图4×4的正方形网格中,△MNP绕某点旋转一定的角度,得到△M1N1P1 , 则其旋转中心可能是( ) A、点A B、点B C、点C D、点D10. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )
A、点A B、点B C、点C D、点D10. 如图,将含有角的直角三角板放置在平面直角坐标系中,在x轴上,若 , 将三角板绕原点O顺时针旋转 , 则点A的对应点的坐标为( )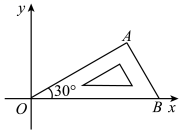 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每空3分,共24分)
-
11. 图中的△ABP是由△ACD按顺时针方向旋转90得到的.这一旋转过程中,旋转中心是点 , 旋转的角度为度,∠PAD=度.
 12. 如图,在中, , , , 将以B为中心逆时针方向旋转,得到 , 当点C的对应点E落在边AB上时,线段AD的长度值是 .
12. 如图,在中, , , , 将以B为中心逆时针方向旋转,得到 , 当点C的对应点E落在边AB上时,线段AD的长度值是 . 13. 如图,将 绕点A逆时针旋转55°得到 ,若 且 于点F,则 .
13. 如图,将 绕点A逆时针旋转55°得到 ,若 且 于点F,则 . 14. 如图,将△ABC绕直角顶点C逆时针旋转,使得点B落在斜边AB上的B'处得△A'B'C,若∠A=35°,则∠BCB'的度数为 .
14. 如图,将△ABC绕直角顶点C逆时针旋转,使得点B落在斜边AB上的B'处得△A'B'C,若∠A=35°,则∠BCB'的度数为 . 15. 如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE , 直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF , 连接EF . 若AB=3,AC=2,且α+β=∠B , 则EF= .
15. 如图,将Rt△ABC的斜边AB绕点A顺时针旋转α(0°<α<90°)得到AE , 直角边AC绕点A逆时针旋转β(0°<β<90°)得到AF , 连接EF . 若AB=3,AC=2,且α+β=∠B , 则EF= . 16. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:
16. 如图,已知△ABC , ∠ABC<60°,将△ABC绕点A逆时针旋转60°得到△ADE , DE与BC交于点P . 下列结论:①∠EPC=60°;
②AC与DE互相平分;
③PA+PC=PE;
④PA平分∠BPE , 其中正确结论的是 .

三、作图题(共3题,共28分)
-
17. 如图,△AOB的三个顶点都在网格的格点上,网格中的每个小正方形的边长均为一个长度单位,以点O建立平面直角坐标系.
 (1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标.18. 如图所给的方格纸中,每个小正方形边长都是1,△ABC是格点三角形(顶点在方格顶点上的三角形叫做格点三角形).
(1)、画出△AOB绕点O逆时针旋转90°后所得的图形△A1OB1;(2)、写出点A1 , B1的坐标.18. 如图所给的方格纸中,每个小正方形边长都是1,△ABC是格点三角形(顶点在方格顶点上的三角形叫做格点三角形). (1)、在图1中画出将△ABC以点A为旋转中心,逆时针旋转90°得到的图形.(2)、在图2中画出△DEF,使△DEF与△ABC全等,且顶点A,B,C,D,E,F在同一个圆上.19. 如图,在平面直角坐标系中, ABC的三个顶点坐标分别为A(-4,-2)、B(-2,0)、C(0,-3), A1B1C是 ABC绕点C顺时针旋转90°后得到的图形.
(1)、在图1中画出将△ABC以点A为旋转中心,逆时针旋转90°得到的图形.(2)、在图2中画出△DEF,使△DEF与△ABC全等,且顶点A,B,C,D,E,F在同一个圆上.19. 如图,在平面直角坐标系中, ABC的三个顶点坐标分别为A(-4,-2)、B(-2,0)、C(0,-3), A1B1C是 ABC绕点C顺时针旋转90°后得到的图形. (1)、写出A1 , B1的坐标;(2)、在所给的平面直角坐标系中画出 A1B1C;(3)、若点B2与点B1关于原点对称,写出A1B2的长.
(1)、写出A1 , B1的坐标;(2)、在所给的平面直角坐标系中画出 A1B1C;(3)、若点B2与点B1关于原点对称,写出A1B2的长.四、解答题(共4题,共38分)
-
20. 如图,正方形网格中每个方格边长为1,△ABC和△A′B′C的顶点均在格点上,并且△A′B′C是由△ABC旋转得到的.根据所给信息,填空:
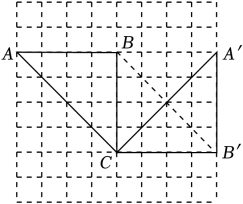 (1)、旋转中心为点 、旋转角的度数为 °、旋转方向为 (顺时针或逆时针);(2)、连结BB′,则四边形ACB′B的形状是 , 面积是 .
(1)、旋转中心为点 、旋转角的度数为 °、旋转方向为 (顺时针或逆时针);(2)、连结BB′,则四边形ACB′B的形状是 , 面积是 .


