浙教版数学八年级暑假知识训练：正方形的性质与判定

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列四边形中，对角线互相垂直平分的是（）

A、平行四边形、菱形 B、矩形、菱形 C、矩形、正方形 D、菱形、正方形

查看试题解析
2. 平行四边形、矩形、菱形、正方形都具有的性质是（　　）

A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等

查看试题解析
3. 在下列命题中，正确的是 ( )

A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形

查看试题解析
4. 如图，四边形ABCD是平行四边形，下列说法不正确的是（）

A、当AC=BD时，四边形ABCD是矩形 B、当AB=BC时，四边形ABCD是菱形 C、当AC平分∠BAD时，四边形ABCD是菱形 D、当∠DAB= 90°时，四边形ABCD是正方形

查看试题解析
5. 如图，在矩形ABCD内有一点F，BF与CF分别平分 $∠ A B C$ 和 $∠ B C D . E$ 为矩形ABCD外一点，连结BE，CE．有下列条件：
① $E B / / C F, C E / / B F$ ；
② $B E = C E, B E = B F$ ；
③ $B E / / C F, C E ⊥ B E$ ；
④ $B E = C E, C E / / B F$ ．
其中能判定四边形BECF是正方形的条件是（）

A、①② B、②③ C、②③④ D、①②③④

查看试题解析
6. 如图，矩形内有两个相邻的白色正方形，其面积分别为2和18，则图中阴影部分的面积为（）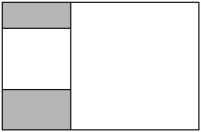

A、 $2 \sqrt{2}$ B、 $4 \sqrt{2}$ C、4 D、6

查看试题解析
7. 如图，在平面直角坐标系中，点C位于第一象限，点B位于第四象限，四边形OABC 是边长为1的正方形，OC与x轴正半轴的夹角为15°，则点B的纵坐标为（）

A、-2 B、 $- \frac{\sqrt{2}}{2}$ C、 $- \frac{1}{2}$ D、 $- \frac{\sqrt{2}}{3}$

查看试题解析
8. 已知四边形ABCD是平行四边形，再从①AB=BC，②∠ABC=90°，③AC=BD，④AC⊥BD四个条件中，选两个作为补充条件后，使得四边形ABCD是正方形，现有下列四种选法，其中错误的是（）

A、选①② B、选②③ C、选①③ D、选②④

查看试题解析
9.
如图，已知在正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，给出下列结论：
①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF．
其中结论正确的共有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 七巧板是我国祖先的一项卓越创造，如图1，正方形ABCD可以制作一副七巧板，现将这副七巧板拼成如图2所示的“风车”造型(内部有一处空缺)，连结最外围的风车顶点 M，N，P，Q得到一个四边形MNPQ，则正方形ABCD与四边形MNPQ的面积之比为（）

A、5：8 B、3 ： 5 C、8： 13 D、25：49

查看试题解析

二、填空题（每题3分，共18分）

11. 边长为 $5 c m$ 的正方形的对角线长为 $c m$ ．

查看试题解析
12. 小明在学习完四边形后，整理成如图所示的知识结构图，发现通过添加边、角或对角线等元素的特殊条件，就能得到特殊的四边形．写出条件①中你认为合适的边、角或对角线的条件是．（写出一个即可）

查看试题解析
13. 如图，三个边长均为2的正方形重叠在一起，O₁，O₂是其中两个正方形的中心，则阴影部分的面积是.

查看试题解析
14. 如图， ▱ ABCD的对角线AC，BD 相交于点O，∠BAO=∠DAO.若添加一个条件使 ▱ ABCD为正方形，则可以添加的条件是.

查看试题解析
15. 如图，定义：若菱形 AECF 与正方形ABCD的两个顶点A，C重合，另外两个顶点E，F在正方形ABCD 的内部，则称菱形AECF 为正方形ABCD 的内含菱形.若正方形的周长为16，其内含菱形的边长是整数，则内含菱形的周长为；若正方形的面积为18，其内含菱形的面积为6，则内含菱形的边长为.

查看试题解析
16. 图1是由两个全等直角三角形和两个长方形组成的□ABCD ，将其剪拼成不重叠，无缝隙的大正方形（如图2）.记①，②，③，④的面积分别为S₁ ， S₂ ， S₃ ， S₄ ，已知S₃=4S₂.

(1)、 $S_{1}^{} : S_{2}^{}$ =；

(2)、若□ABCD的周长比长方形③的周长大18，则BC为．

查看试题解析

三、作图题（共9分）

17. 定义：在边长为1的小正方形方格纸中，把顶点落在方格交点上的线段、三角形、四边形分别称为格点线段、格点三角形、格点四边形，在5×5的正方形网格中，若每一个小正方形的边长均为1，请仅用无刻度直尺按要求画图．

(1)、在图①中画一个以AB为边画一个格点正方形ABCD；

(2)、在图②中画一个格点平行四边形AEBF ，使平行四边形面积为6；

(3)、在图③中画一个格点菱形AMBN ， AMBN不是正方形．
（提示：请画在答题卷相对应的图上）

查看试题解析

四、解答题（共7题，共63分）

18. 如图，在正方形ABCD中，点E，F为对角线BD上两点，CE=CF．

(1)、求证：AE=CE

(2)、请你判断四边形AFCE的形状，(不必证明)

(3)、若EF=6，DE=BF=3，求四边形AECF的周长．

查看试题解析
19. 如图，在正方形ABCD中，AB=4，点E是对角线AC上的一点，连结DE．过点E作EF⊥ED，交AB于点F，以DE ，EF为邻边作矩形DEFG，连结AG．

(1)、求证：矩形DEFG是正方形；

(2)、求AG+AE的值；

(3)、若F恰为AB的中点，请求出AE的长．

查看试题解析
20. 如图，在平行四边形ABCD中，AD=9 cm，CD= $3 \sqrt{2}$ cm，∠B=45°，点M，N分别以A，C为起点，以1 cm/s的速度沿AD，CB边运动，设点M，N运动的时间为t s(0≤t≤6)．．

(1)、求BC边上的高AE的长度．

(2)、连结AN，CM，当t为何值时，四边形AMCN为菱形？

(3)、作MP⊥BC于点P，NQ⊥AD于点Q，当t为何值时，四边形MPNQ为正方形？

查看试题解析
21. 如图，在正方形ABCD中，E，F 分别是BC，CD 上的点，AE，BF 相交于点P，并且AE=BF.

(1)、如图1，判断AE和BF 的位置关系，并说明理由.

(2)、若AB=8，BE=6，求BP的长度.

(3)、如图2，作 DN⊥AE于点N，FM⊥DN于点M，当点F 在线段CD 上运动时(点 F 不与C，D 两点重合)，四边形 FMNP 能否成为正方形? 请说明理由.

查看试题解析
22. 如图1，两张纸片正方形 $A B C D$ 与正方形 $B E F G$ 拼在一起，在 $A B$ 边上取 $A M = B E$ ，沿 $D M$ ， $M F$ 分别剪一刀，将 $△ D A M$ 拼至 $△ D C N$ ， $△ M E F$ 拼至 $△ N G F$ ，无缝隙无重叠，如图2．

(1)、求证： $D M = M F$ ．

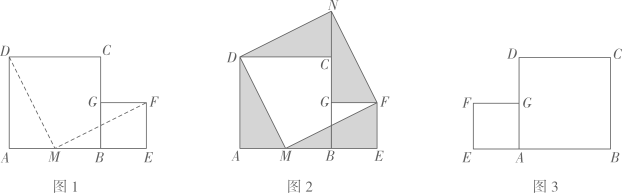(2)、求证：四边形 $D M F N$ 是正方形．

(3)、仿照题中的剪拼方法，剪两刀把图3中两个正方形剪拼成一个更大的正方形，在图中作出剪拼线，并完成拼图．

查看试题解析
23. 定义：一个四边形的四条边和两条对角线这六条线段中只有两种长度，我们把这样的四边形叫做双距四边形．

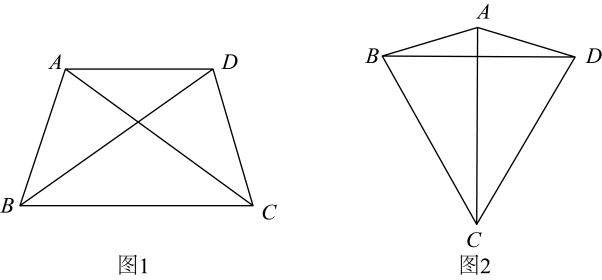(1)、下列说法正确的有（填序号）．
①正方形一定是双距四边形．
②矩形一定是双距四边形．
③有一个内角为 $60 °$ 的菱形是双距四边形．

(2)、如图1，在四边形 $A B C D$ 中， $A D ∥ B C$ ， $A B = A D$ ， $∠ A B C = ∠ D C B = 72 °$ ，求证：四边形 $A B C D$ 为双距四边形．

(3)、如图2，四边形 $A B C D$ 为双距四边形， $A B = A D = \sqrt{6}$ ， $B C = D C$ ， $A B < B C$ ，求 $B C$ 的长．

查看试题解析
24. 如图1，矩形ABCD中，过对角线AC的中点O画EF⊥AC分别交AB，CD于点E，F，连结AF，CE．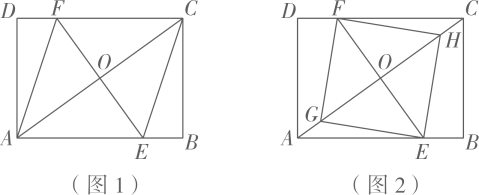

(1)、[证明体验]
求证：四边形AECF是菱形．

(2)、[基础巩固]
若AB=8，BC=6，求菱形AECF的边长．

(3)、[拓展延伸]
如图2，在对角线AC上取点G，H，使得四边形EHFG是正方形，若正方形EHFG的边长为 $3 \sqrt{2}$ ，且AE=5CH，求矩形ABCD的面积．

查看试题解析