浙教版数学八年级暑假知识训练:菱形的性质与判定
试卷更新日期:2024-06-30 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 矩形具有而菱形不一定有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角相等2. 已知四边形ABCD是菱形,则下列结论中,不一定正确的是( )A、∠A=∠B=∠C=∠D B、AB=BC=CD=DA C、AC⊥BD D、AC平分∠BAD和∠BCD3. 下列条件中,能判定四边形是菱形的是( )A、两条对角线相等 B、两条对角线互相垂直 C、两条对角线互相垂直平分 D、两条对角线相等且互相垂直4. 如图,将△ABC沿BC方向平移得到△DCE,连结BD,AD,下列条件不能判定四边形ABCD是菱形的是( )
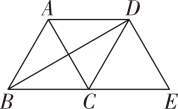 A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD5. 用直尺和圆规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )A、
A、∠ABC=∠ACB B、AB=AD C、∠BAC=∠DAC D、AC⊥BD5. 用直尺和圆规在一个平行四边形内作菱形ABCD,下列作法中,错误的是( )A、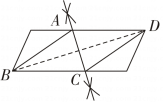 B、
B、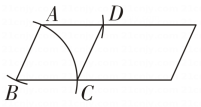 C、
C、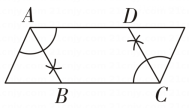 D、
D、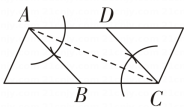 6. 如图,菱形ABCD的对角线AC , BD相交于点O , 过点B作BE⊥AD于点E , 连接OE , 若菱形ABCD的面积为16,OA=4,则OE的长为( )
6. 如图,菱形ABCD的对角线AC , BD相交于点O , 过点B作BE⊥AD于点E , 连接OE , 若菱形ABCD的面积为16,OA=4,则OE的长为( ) A、3 B、2.5 C、 D、27. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为CD的中点.若OE=3,则菱形ABCD的周长为( )
A、3 B、2.5 C、 D、27. 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为CD的中点.若OE=3,则菱形ABCD的周长为( ) A、6 B、12 C、24 D、488. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( )
A、6 B、12 C、24 D、488. 如图,在菱形ABCD中,AC,BD相交于点O,E为AB的中点,且DE⊥AB,AC=6,则菱形ABCD的面积是( ) A、18 B、18 C、9 D、69. 如图,□ABCD的对角线相交于点O,M,N分别是边AD,BC 的中点,连结AN,CM.有下列两个结论:①若四边形 ANCM 是菱形,则AB⊥AC;②若四边形 ANCM 是矩形,则AB=AC.那么 ( )
A、18 B、18 C、9 D、69. 如图,□ABCD的对角线相交于点O,M,N分别是边AD,BC 的中点,连结AN,CM.有下列两个结论:①若四边形 ANCM 是菱形,则AB⊥AC;②若四边形 ANCM 是矩形,则AB=AC.那么 ( ) A、①正确,②错误 B、①错误,②正确 C、①②都正确 D、①②都错误10. 在数学课拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长是1,且一个内角是60°的小菱形拼成的图形,P是其中4个小菱形的公共顶点,小新在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A、①正确,②错误 B、①错误,②正确 C、①②都正确 D、①②都错误10. 在数学课拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长是1,且一个内角是60°的小菱形拼成的图形,P是其中4个小菱形的公共顶点,小新在小明的启发下,将该图形沿着过点P的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )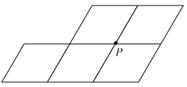 A、2 B、3 C、 D、
A、2 B、3 C、 D、二、填空题(每题4分,共24分)
-
11. 如图,在菱形ABCD中,AB=10cm,AC=16cm,E,F分别是CD和BC的中点,连结EP并延长与AB的延长线相交于点G,则EG的长度为cm
 12. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF,AD=10,EF=4,则BG的长为.
12. 如图,菱形ABCD的对角线AC,BD相交于点O,E是AD的中点,点F,G在AB上, EF⊥AB,OG∥EF,AD=10,EF=4,则BG的长为. 13. 已知菱形ABCD的面积为20cm²,对角线AC的长为8cm,则对角线BD的长为cm.14. 如图,在正三角形ABC中,D,E,F分别是三边的中点.图中有个正三角形,有个菱形.
13. 已知菱形ABCD的面积为20cm²,对角线AC的长为8cm,则对角线BD的长为cm.14. 如图,在正三角形ABC中,D,E,F分别是三边的中点.图中有个正三角形,有个菱形. 15. 如图,有两张矩形纸片 ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示的方式叠放,使点D 与点G 重合,且重叠部分为▱MNDK.若两张纸片交叉所成的角记为α,则当a=30°时,BM=cm;当α最小时,重叠部分的面积为cm2.
15. 如图,有两张矩形纸片 ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.将两纸片按如图所示的方式叠放,使点D 与点G 重合,且重叠部分为▱MNDK.若两张纸片交叉所成的角记为α,则当a=30°时,BM=cm;当α最小时,重叠部分的面积为cm2.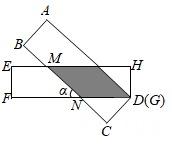 16. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 .
16. 小明同学学习了菱形的知识后,结合之前学习的赵爽弦图,编了一个菱形版“赵爽弦图”如图,菱形中, , 四边形是矩形,若 , 则矩形的面积为 .
三、作图题(共8分)
-
17. 如图,16个形状大小完全相同的菱形组成网格 , 菱形的顶点称为格点.
 (1)、在图1中画出矩形 , 使得 , , , 分别落在 , , , 边包含端点的格点上画出其中一个即可 .(2)、如图2,已知点 , , , , 均在格点上,请在网格中包含边界找一格点 , 连结 , 使得直线平分平行四边形的面积.
(1)、在图1中画出矩形 , 使得 , , , 分别落在 , , , 边包含端点的格点上画出其中一个即可 .(2)、如图2,已知点 , , , , 均在格点上,请在网格中包含边界找一格点 , 连结 , 使得直线平分平行四边形的面积.四、解答题(共7题,共58分)
-
18. 小惠自编一题:“如图,在四边形ABCD中,对角线AC,BD相交于点O,AC⊥BD,OB=OD.求证:四边形ABCD是菱形”,并将自己的证明过程与同学小洁交流.
小惠:
证明:∵AC⊥BD,OB=OD,
∴AC垂直平分BD,
∴AB=AD,CB=CD,
∴四边形ABCD是菱形.
小洁:
这个题目还缺少条件,需要补充一个条件才能证明.
若赞同小惠的证法,请在第一个方框“”内打“√" ;若赞成小洁的说法,请你补充一个条件,并证明.19. 如图,在菱形ABCD中,F为边AB的中点,FC与对角线BD相交于点C,过点G作GE⊥BC于点E,∠ADB=∠FCB.求证: (1)、AB=2BE;(2)、DG=CF+GE.20. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.
(1)、AB=2BE;(2)、DG=CF+GE.20. 如图,菱形ABCD的对角线相交于点O,BE∥AC,AE∥BD,EO与AB相交于点F.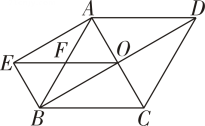 (1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.21. 如图,在四边形ABCD中,AB∥CD,点E,F在对角线BD上,BE=EF=FD,∠BAF=∠DCE=90°.
(1)、求证:EO=DC;(2)、若菱形ABCD的边长为10,∠EBA=60°,求菱形ABCD的面积.21. 如图,在四边形ABCD中,AB∥CD,点E,F在对角线BD上,BE=EF=FD,∠BAF=∠DCE=90°. (1)、求证:△ABF≌△CDE.(2)、连结AE,CF,已知 ▲ (从条件①:∠ABD=30°.条件②:AB=BC中选择一个作为已知,填序号),请判断四边形AECF的形状,并说明理由.22. 如图,在平行四边形ABCD中,AB=5,BC=7,∠ACB=45°,AC>AB , E , F为对角线AC上的两点(点E与A、C、F都不重合),AE=CF , EM⊥BC于点M , FN⊥AD于点N , 连结EN , FM .
(1)、求证:△ABF≌△CDE.(2)、连结AE,CF,已知 ▲ (从条件①:∠ABD=30°.条件②:AB=BC中选择一个作为已知,填序号),请判断四边形AECF的形状,并说明理由.22. 如图,在平行四边形ABCD中,AB=5,BC=7,∠ACB=45°,AC>AB , E , F为对角线AC上的两点(点E与A、C、F都不重合),AE=CF , EM⊥BC于点M , FN⊥AD于点N , 连结EN , FM . (1)、求证:四边形EMFN是平行四边形.(2)、四边形EMFN能否成为矩形?四边形EMFN能否成为菱形?请直接写出答案.(3)、连结MN , 作点C关于MN的对称点C' , 若点C'落在边AB上,求AE的长.23. 在平行四边形中, , , .
(1)、求证:四边形EMFN是平行四边形.(2)、四边形EMFN能否成为矩形?四边形EMFN能否成为菱形?请直接写出答案.(3)、连结MN , 作点C关于MN的对称点C' , 若点C'落在边AB上,求AE的长.23. 在平行四边形中, , , . (1)、若 , 则;(2)、如图 , 当时,求对角线的长(用含的式子表示);(3)、如图 , 四边形 , 四边形都是平行四边形,延长交于点 , 若 , , , , 求的长.24. 【问题情境】
(1)、若 , 则;(2)、如图 , 当时,求对角线的长(用含的式子表示);(3)、如图 , 四边形 , 四边形都是平行四边形,延长交于点 , 若 , , , , 求的长.24. 【问题情境】在“综合与实践”活动课上,老师给出了如图1所示的一张矩形纸片ABCD,其中.如图2,将矩形纸片ABCD沿对角线AC剪开,得到纸片与.
 (1)、【实践探究】
(1)、【实践探究】将纸片沿AC方向平移,连结与AC相交于点 , 得到图3所示的图形.若 , 解答下列问题:
①求证:.
②求出平移的距离.
(2)、【拓展延伸】如图4,先将纸片沿AC方向平移一定距离,然后将纸片绕点顺时针旋转,使 , 若此时恰好经过点 , 求出平移的距离.
-