浙教版数学八年级暑假知识训练：矩形的性质与判定

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 矩形具有而一般平行四边形不具有的性质是（）

A、对角线相等 B、对角相等 C、对边相等 D、对角线互相平分

查看试题解析
2. 下列说法正确的是（）

A、有一个角是直角的四边形是矩形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是矩形 D、四个角都是直角的四边形是矩形

查看试题解析
3. 顺次连结菱形四边中点得到的四边形是（）

A、一般的平行四边形 B、菱形 C、矩形 D、只有一组对边平行的四边形

查看试题解析
4. 已知矩形的一边长为6cm，一条对角线的长为10 cm，则矩形的面积为（）

A、12 cm² B、24 cm² C、48 cm² D、60 cm²

查看试题解析
5. 如图，矩形ABCD的对角线AC，BD相交于点O，AB=6，∠ACB=30°，则OD的长为（）

A、6 B、8 C、10 D、12

查看试题解析
6.
如图，在矩形ABCD中，对角线AC，BD相交于点O，AE⊥BD，垂足为E，AE=3，ED=3BE，则AB的值为（　　）

A、6 B、5 C、 $2 \sqrt{3}$ D、 $3 \sqrt{3}$

查看试题解析
7. 如图，EF过矩形ABCD对角线的交点O，且分别交AB，CD 于点E，F，则阴影部分的面积是矩形ABCD 面积的（）

A、 $\frac{1}{5}$ B、 $\frac{1}{4}$ C、 $\frac{3}{10}$ D、 $\frac{1}{3}$

查看试题解析
8. 如图，在矩形ABCD 中(AD>AB)，E是边 BC 上一点，且 DE=DA.若 AF⊥DE，垂足为 F，则下列结论中，不一定正确的是（）

A、AB=AF B、 $A F = \frac{1}{2} A D$ C、△AFD≌△DCE D、BE=AD-DF

查看试题解析
9. 如图，在 Rt△ABC中，∠ACB=90°，AC=3，BC=4，M 是边 AB 上一点(不与点 A，B 重合)，过点 M 作ME⊥AC 于点E，MF⊥BC 于点 F.若 P 是EF 的中点，则CP的最小值为（）

A、1.2 B、1.5 C、2.4 D、2.5

查看试题解析
10. 如图，在 ▱ ABCD中，有下列条件：①AC=BD.②∠1+∠3=90°.③OB= $\frac{1}{2}$ AC.④∠1=∠2.其中能判定 ▱ ABCD是矩形的有（）

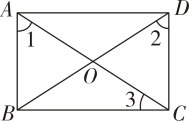A、① B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题（每题4分，共24分）

11. 如图，在矩形 ABCD的边AD 上找一点 P，使点 P 到B，C两点的距离之和最短，则点 P 的位置应该在.

查看试题解析
12. 如图，在矩形ABCD中，AC，BD相交于点O，M，N 分别为BC，OC 的中点，若MN=4，则AO 的长为

查看试题解析
13.
如图，在矩形ABCD中，BC=20cm，点P和点Q分别从点B和点D出发，按逆时针方向沿矩形ABCD的边运动，点P和点Q的速度分别为3cm/s和2cm/s，则最快 s后，四边形ABPQ成为矩形．

查看试题解析
14. 如图，已知在 Rt△ABC中，∠ABC=90°，小明按如下步骤作图：①以点 A 为圆心，BC长为半径作弧，以点 C为圆心，AB长为半径作弧，两弧相交于点 D；②连结 DA，DC，则四边形ABCD为形，判定的依据是.

查看试题解析
15. 如图，在矩形纸片 ABCD中，AB=6cm，BC=8cm，现要在纸片上剪下一个腰长为5cm 的等腰三角形AEF，点 E，F 在矩形的边上，则剪下的等腰三角形 AEF 的面积为cm².

查看试题解析
16. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $B C = 2 \sqrt{5}$ ， $A C = \sqrt{5}$ ，点 $D$ 在 $A B$ 上， $A D = 1$ ，现将一个足够大的三角板的直角顶点与点 $D$ 重合，并绕着点 $D$ 转动，三角板的两直角边分别与 $A C$ 、 $B C$ 交于点 $E$ 、 $F$ ，连结 $E F$ ，以 $E D$ 、 $E F$ 为邻边作平行四边形 $D E F G$ ，在转动过程中，当线段 $E F$ 的长度最小时，平行四边形 $D E F G$ 的面积为.

查看试题解析

三、作图题（共2题，共13分）

17. 规定：每个顶点都在格点的四边形叫做格点四边形．在 $10 \times 6$ 的正方形网格中画出符合要求的格点四边形（每个小正方形的边长为1）．

(1)、在图1中画出一个以 $A B$ 为边的平行四边形．

(2)、在图2中画出一个以 $A B$ 为对角线的矩形，且它的周长为无理数．

查看试题解析
18. 如图是由全等的小菱形组成的 $3 \times 3$ 网格，点A，B，P均在格点上， $P B = 1$ ， $A B = \sqrt{3}$ ．

(1)、求证： $A B ⊥ P B$ ；

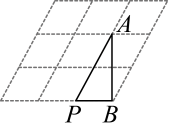(2)、请你画出一个顶点都在格点上且面积最大的矩形；

(3)、满足（2）中条件的矩形一共能画出个．

查看试题解析

四、解答题（共6题，共53分）

19. 如图，将 $▱ A B C D$ 的边AB延长到点E ，使 $B E = A B$ ，连结DE ，交边BC于点F ．

(1)、求证： $△ B E F ≌ △ C D F$ ．

(2)、连结BD ， CE ．若 $∠ B F D = 2 ∠ A$ ，求证：四边形BECD是矩形．

查看试题解析
20. 如图，在△ABC中，AC=9，AB=12，BC=15，P 为边 BC上一动点，PG⊥AC 于点G，PH⊥AB 于点H.

(1)、求证：四边形 AGPH 是矩形.

(2)、在点 P 的运动过程中，GH 的长是否存在最小值? 若存在，请求出最小值；若不存在，请说明理由.

查看试题解析
21. 在 $▱ A B C D$ 中，E，F为 $B C$ 上的两点，且 $B E = C F$ ， $A F = D E$ ．

(1)、求证： $Δ A B F ≌ Δ D C E$ ；

(2)、求证： $▱ A B C D$ 是矩形；

(3)、连接 $A E$ ，若 $A F$ 是 $∠ E A D$ 的平分线， $B E = 2$ ， $A F = \sqrt{30}$ ，求四边形 $A B C D$ 的面积．

查看试题解析
22. 在四边形 $A B C D$ 中， $A B ∥ C D ， ∠ B C D = 90 ° ， A B = A D = 10 c m ， B C = 8 c m$ ，点P从点A出发，沿折线 $A B C D$ 方向以 $3 c m / s$ 的速度匀速运动；点Q从点D出发，沿线段 $D C$ 方向以 $2 c m / s$ 的速度匀速运动.已知两点同时出发，当一个点到达终点时，另一点也停止运动，设运动时间为 $t (s)$ .

(1)、求 $C D$ 的长；

(2)、当四边形 $P B Q D$ 为平行四边形时，求四边形 $P B Q D$ 的周长；

(3)、在点P、Q的运动过程中，是否存在某一时刻，使得 $△ B P Q$ 的面积为 $16 c m^{2}$ ？若存在，请求出所有满足条件的t的值；若不存在，请说明理由.

查看试题解析
23. 如图，在长方形 $ABCD$ 中，边 $AB$ 、 $BC$ 的长 $(AB < BC)$ 是方程 $x^{2} - 7 x + 12 = 0$ 的两个根.点 $P$ 从点 $A$ 出发，以每秒 $1$ 个单位的速度沿 $△ ABC$ 边 $A \to B \to C \to A$ 的方向运动，运动时间为 $t ($ 秒 $)$ .

(1)、求 $AB$ 与 $BC$ 的长；

(2)、当点 $P$ 运动到边 $BC$ 上时，试求出使 $AP$ 长为 $\sqrt{10}$ 时运动时间 $t$ 的值；

(3)、当点 $P$ 运动到边 $AC$ 上时，是否存在点 $P$ ，使 $△ CDP$ 是等腰三角形？若存在，请求出运动时间 $t$ 的值；若不存在，请说明理由.

查看试题解析
24. 如图，在矩形ABCD中，AB=6 ， BC=8 ，将矩形ABCD绕点D按顺时针方向旋转，得到矩形EFGD ，直线DE ， FG分别与直线BC交于点P ， Q.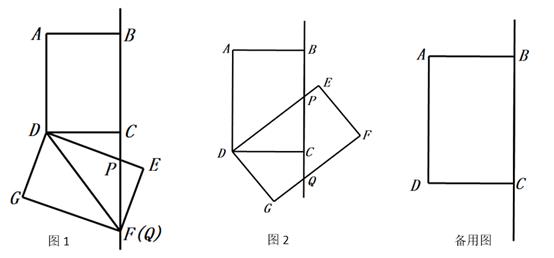

(1)、如图1，当矩形EFGD的顶点F落在线段BC的延长线上时，求DP的长．

(2)、如图2，在矩形旋转过程中，当P位于线段BC上时，求证：DP=PQ.

(3)、在旋转过程中，旋转角 $α$ 满足 $0^{\circ} < α \leq 90^{\circ}$ ，当 $B P = \frac{1}{2} B Q$ 时，求CP的长（直接写出答案）.

查看试题解析