浙教版数学八年级暑假知识训练：反证法

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 用反证法证明某个命题的结论“ $a > 0$ ”时，第一步应假设（）

A、 $a < 0$ B、 $a \neq 0$ C、 $a \geq 0$ D、 $a \leq 0$

查看试题解析
2. 用反证法证明“在 $△ A B C$ 中，若 $A B = A C$ ，则 $∠ B = ∠ C$ ”时，则应假设（）

A、 $∠ A = ∠ B$ B、 $∠ B \neq ∠ C$ C、 $A B \neq A C$ D、 $B C = A C$

查看试题解析
3. 若用反证法证明命题“四边形中至少有一个角是钝角或直角”时，则首先应该假设这个四边形中（）

A、至少有一个角是钝角或直角 B、没有一个角是锐角 C、没有一个角是钝角或直角 D、每一个角都是钝角或直角

查看试题解析
4. 用反证法证明命题：“等腰三角形的底角是锐角”时，第一步可以假设（）

A、底角为锐角的三角形是等腰三角形 B、等腰三角形的底角是直角 C、等腰三角形的底角是钝角 D、等腰三角形的底角是直角或钝角

查看试题解析
5. 牛顿曾说过：“反证法是数学家最精良的武器之一”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于 $60 °$ ”时，第一步先假设（）

A、三角形中有一个内角小于 $60 °$ B、三角形中有一个内角大于 $60 °$ C、三角形中没有一个内角小于 $60 °$ D、三角形中每个内角都大于 $60 °$

查看试题解析
6. 用反证法证明“在△ABC中，若∠A＞∠B＞∠C ，则∠A＞60°”时，应先假设（　　）

A、∠A＝60° B、∠A＜60° C、∠A≠60° D、∠A≤60°

查看试题解析
7. 假设命题“ $a > 0$ ”不成立，那么 $a$ 与0的大小关系只能是（）

A、 $a \neq 0$ ． B、 $a < 0$ ． C、 $a = 0$ ． D、 $a ⩽ 0$ ．

查看试题解析
8. 用反证法证明命题“如图，如果 AB∥CD，AB ∥EF，那么CD∥EF”时，第一步是（）

A、假设 AB不平行于CD B、假设 AB不平行于 EF C、假设 CD∥EF D、假设 CD不平行于 EF

查看试题解析
9. 下列说法中，正确的是（）

A、不等式 $x < \frac{7}{3}$ 只有2个解 B、不等式 $x + 5 > 3$ 的解集为 $x > 2$ C、用反证法证明“三角形中必有一个内角不小于60°”时，首先应假设：这个三角形中每一个内角都大于60° D、有两个角相等的等腰三角形是等边三角形

查看试题解析
10. 已知命题“在△ABC中，若AB=AC，则∠B<90°”.下面写出运用反证法证明这个命题的四个打乱顺序的步骤：
①∴∠A+∠B+∠C>180°，这与三角形内角和为 180°矛盾.
②因此假设不成立，∴∠B<90°.
③假设在△ABC中，∠B≥90°.
④由 AB=AC，得∠B=∠C≥90°，即∠B+∠C≥180°.
这四个步骤正确的顺序应是（）

A、④③①② B、③④②① C、①②③④ D、③④①②

查看试题解析

二、填空题（每题4分，共24分）

11. 用反证法证明命题“在△ABC中，若∠A＞∠B＋∠C，则∠A＞90°”时，应先假设.

查看试题解析
12. 用反证法证明“ $x < 3$ ”时，首先应假设．

查看试题解析
13. 命题“若 $△ A B C$ 中，如果 $A C^{2} + B C^{2} \neq A B^{2}$ ，那么 $∠ C \neq 90 °$ ”，用反证法证明此命题时，应首先假设成立．

查看试题解析
14. 用反证法证明命题“若a，b是整数，且ab能被5整除，则a，b中至少有一个能被5整除”时，应先假设.

查看试题解析
15. 对于命题“如图，如果OA＝OC，OB≠OD，那么四边形ABCD不是平行四边形”．用反证法证明这个结论时，第一步应假设．

查看试题解析
16. 用反证法证明（填空）：
已知：如图， $∠ 1, ∠ 2$ 是直线 $l_{1}, l_{2}$ 被直线 $l_{3}$ 截得的内错角， $l_{1}$ 与 $l_{2}$ 不平行．
求证： $∠ 1 \neq ∠ 2$ ．
证明：假设 $∠ 1 = ∠ 2$ ，
那么 $l_{1}$ $l_{2} ($ ），这与相矛盾，所以不能成立，即所求证的命题 $∠ 1 \neq ∠ 2$ 正确．

查看试题解析

三、证明题（共8题，共66分）

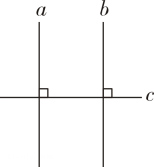
17. 如图，已知a⊥c，b⊥c，用反证法证明：a∥b.

查看试题解析
18. [推理能力]已知任何一个有理数均可表示成b/a的形式，且a，b互质.求证： $\sqrt{5}$ 是一个无理数(请用反证法证明)

查看试题解析
19. 已知a，b，c，d四个数满足 $a + b = 1, c + d = 1, a c + b d > 1$ ．求证：这四个数中至少有一个负数．

查看试题解析
20. 已知：如图，在 $△ A B C$ 中，点D，E分别在AC，AB上，BD，CE相交于点 $O$ ．求证：BD和CE不可能互相平分．

查看试题解析
21. 用反证法证明：三角形的一个外角等于与它不相邻的两个内角的和.
解：已知：如图所示，∠ACD是△ABC的一个外角.
求证：∠ACD=∠A+∠B.

查看试题解析
22. 如图，在△ABC中，AB=AC，P是△ABC内的一点，且∠APB>∠APC，求证：PB<PC．(用反证法)

查看试题解析
23. 用反证法证明：三角形的一个外角等于与它不相邻的两个内角的和.

查看试题解析

24. 阅读下列文字，回答问题．

题目：在Rt $△ A B C$ 中， $∠ C = 9 0^{°}, ∠ A \neq 4 5^{°}$ ，则 $A C \neq B C$ ．

证明：假设 $A C = B C$ ，因为 $∠ A \neq 4 5^{°}, ∠ C = 9 0^{°}$ ，所以 $∠ A \neq ∠ B$ ．

所以 $A C \neq B C$ ，这与假设矛盾，所以 $A C \neq B C$ ．

上面的证明有没有错误？若没有错误，指出其证明的方法；若有错误，请予以纠正．

查看试题解析