浙教版数学八年级暑假知识训练：多边形
试卷更新日期：2024-06-30 类型：复习试卷
一、选择题（每题3分，共30分）
-
1. 某多边形的内角和是其外角和的2倍，则此多边形的边数为（ ）A、3 B、4 C、5 D、62. 已知一个多边形的内角和等于外角和的3倍，则这个多边形为（ ）A、五边形 B、六边形 C、七边形 D、八边形3. 若一个多边形的每一个外角都是36°，则该多边形的边数为（ ）A、7 B、8 C、9 D、104. 若一个多边形的内角和为1260°，则这个多边形的边数为（ ）A、6 B、7 C、8 D、95. 一个多边形的内角和等于它的外角和的2倍，则这个多边形是（ ）A、四边形 B、五边形 C、六边形 D、七边形6. 一个多边形的内角和与它的外角和的和为 ， 则这个多边形的边数为（ ）A、11 B、10 C、9 D、87. 已知一个多边形的内角和是它的外角和的3倍，则这个多边形是（ ）A、九边形 B、八边形 C、七边形 D、六边形8. 一个多边形从一个顶点最多能引出三条对角线，这个多边形是（ ）A、三角形 B、四边形 C、五边形 D、六边形9. 一个多边形剪去一个角后得到一个新的多边形，则关于这两个多边形，下列量中一定没有发生变化的是（ ）A、内角度数 B、内角和度数 C、对角线条数 D、外角和度数10. 小丽利用最近学习的数学知识，给同伴出了这样一道题：如图，小刚从点 A 出发，沿直线走 6米后向左转θ，接着沿直线前进 6 米后，再向左转θ……如此下去，当他第一次回到点A时，发现自己走了 72米，则θ的度数为（ ）
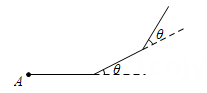A、28° B、30° C、33° D、36°二、填空题（每题4分，共24分）
-
11. 一个多边形的每一个外角都为 ， 则这个多边形是边形．12. 从一个多边形的一个顶点出发可以引5条对角线，这个多边形的边数是 ．13. 若边形的每个内角都为 ， 则等于14. 如果一个n边形的内角和等于它的外角和，则n＝ ．15. 一个多边形的内角和是它的外角和的3倍，则从这个多边形的一个顶点出发共有条对角线.16. 如图，∠1，∠2，∠3，∠4，∠5是五边形ABCDE的外角，且∠1=∠2=∠3=∠4=69°，则∠5=°.
三、解答题（共8题，共66分）
-
17. 如图， ． 若 ， 求的度数．
18. 一个多边形的内角和等于外角和的3倍，它是几边形？19. 一个多边形的内角和比它的外角的和的2倍还大180°，求这个多边形的边数．20. 过多边形一个顶点的所有对角线将这个多边形分成4个三角形．(1)、这个多边形是几边形？(2)、求这个多边形内角和的度数．21. 在凸多边形中, 四边形有2条对角线, 五边形有5条对角线, 经过观察、探索、归纳, 你认为凸八边形的对角线条数应该是多少条? 简单扼要地写出你的思考过程.22.如图，小明从点O出发，前进5m后向右转15°，再前进5m后又向右转15°，…这样一直下去，直到他第一次回到出发点O为止，他所走的路径构成了一个多边形．
(1)、小明一共走了多少米？(2)、这个多边形的内角和是多少度？
