浙教版数学八年级暑假知识训练:一元二次方程的解法
试卷更新日期:2024-06-30 类型:复习试卷
一、选择题(每题3分,共30分)
-
1. 关于x的方程的两个根满足 , 且 , 则m的值为( )A、 B、1 C、3 D、92. 已知关于x的方程(a , b , m均为常数,且)的两个解是 , 则方程的解是( )A、 B、 C、 D、3. 用配方法解一元二次方程时,此方程可变形为( )A、 B、 C、 D、4. 已知方程 可以配方成 的形式,那么 可以配方成下列的( )A、 B、 C、 D、5. 已知关于x的方程 , 当时,方程的解为( )A、 , B、 , C、 D、6. 是下列哪个一元二次方程的根( )A、 B、 C、 D、7. 我们知道方程 的解是 , ,现给出另一个方程 ,它的解是( )A、 , B、 , C、 , D、 ,8. 小李解方程的步骤如图所示,则下列说法正确的是( )
 A、小李解方程的过程正确 B、也是该方程的一个解 C、小李解方程的方法是配方法 D、解方程的过程是从第② 步到第③ 步时出现错误9. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]=x2的解为( )
A、小李解方程的过程正确 B、也是该方程的一个解 C、小李解方程的方法是配方法 D、解方程的过程是从第② 步到第③ 步时出现错误9. 定义[x]表示不超过实数x的最大整数,如[1.8]=1,[﹣1.4]=﹣2,[﹣3]=﹣3.函数y=[x]的图象如图所示,则方程[x]=x2的解为( )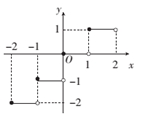 A、0或 B、0或2 C、1或﹣ D、或﹣10. 对于一元二次方程 , 下列说法:
A、0或 B、0或2 C、1或﹣ D、或﹣10. 对于一元二次方程 , 下列说法:若 , 则方程必有一根为;
若方程有两个不相等的实根,则方程无实根;
若方程两根为 , 且满足 , 则方程 , 必有实根 , ;
若是一元二次方程的根,则 .
其中正确的( )
A、 B、 C、 D、二、填空题(每题4分,共24分)
-
11. 若用配方法解方程时,将其配方为的形式,则 .12. 对于两个互不相等的有理数a , b我们规定符号表示a , b两个数中最大的数.按照这个规定则方程的解为 .13. 已知关于的一元二次方程(均为常数,且)的解是 , , 则关于的一元二次方程的解是 .14. 若方程(x2﹣1)(x2﹣4)=k有四个非零实根,且它们在数轴上对应的四个点等距排列,则k= .15. 对于实数a,b,定义新运算“◎”:a◎b=(a+b)²-(a-b)².若(m+2)◎(m-3)=24,则m=16. 定义:若、是方程的两个整数根,且满足 , 则称此类方程为“自然方程”,例如:是“自然方程”.
⑴下列方程是“自然方程”的是;(填序号)
①;②;③ .
⑵若方程是“自然方程”,m的值为 .
三、计算题
-
17. 解方程:(1)、(2)、18. 解方程:(1)、2x﹣6=(x﹣3)2(2)、x2﹣4x﹣7=019. 选择适当的方法解下列方程:(1)、 .(2)、 .(3)、 .
四、解答题(共6分)
-
20.(1)、关于 的方程 , 下列解法完全正确的是 .
甲
乙
两边同时除以
得到 .
移项得 ,
,
,
.
丙
丁
整理得 ,
,
,
,
.
整理得 ,
配方得 ,
,
,
.
(2)、 选择合适的方法解方程五、实践探究题(共4题,共39分)
-
21. 定义一种新运算:对于任意非零实数和 , , 例如: , , 请回答下列问题:(1)、计算;(2)、解方程:(3)、直接写出不等式的解.22. 阅读下列材料:为解方程可将方程变形为然后设 , 则 .
例: ,
解:令 , 原方程化为 , 解得 , ,
当时,(无意义,舍去)
当时, , 解得 ,
原方程的解为 , .
上面这种方法称为“换元法”,把其中某些部分看成一个整体,并用新字母代替(即:换元),则能使复杂的问题转化成简单的问题.
利用以上学习到的方法解下列方程:
(1)、(2)、23. 阅读下列材料:已知实数x , y满足 , 试求的值.
解:设 , 则原方程变为 , 整理得 , , 根据平方根意义可得 , 由于 , 所以可以求得 . 这种方法称为“换元法”,用一个字母去代替比较复杂的单项式、多项式,可以达到化繁为简的目的.
根据阅读材料内容,解决下列问题:
(1)、已知实数x , y满足 , 求的值.(2)、已知a , b满足方程组;求的值;(3)、填空:已知关于x , y的方程组的解是 , 则关于x , y的方程组的解是 .
24. 【综合与实践习】【问题情境】课堂上,老师让同学们复习一元二次方程ax2+bx+c=0(a≠0)的多种解法,在讨论这些解法之间的关系时,小组同学发言如下:
(1)、【操作判断】小彬:分解因式法可以解特殊结构的一元二次方程,基本思路是通过分解因式将方程变形为(x一m)(x一n)=0的形式,这样就可以将原方程化为两个一元一次方程x-m=0或 , 进而得到原方程的根为x1=m,x2=。(2)、【实践探究】小文:分解因式法虽好,但是有些方程用这个方法不太方便,比如 , 这个方程利用公式法或者配方法可得: , 但我们能反过来利用这两个解帮助我们对进行因式分解得到 , 请你利用这个方法对进行因式分解.(3)、【问题解决】小枪:从特殊到一般,是否所有的代数式都能进行因式分解呢?请说明能进行因式分解的代数式中的a,b,c要满足什么条件,因式分解的结果是什么?
-