浙教版数学七年级暑假知识训练：平方差公式及其应用

试卷更新日期：2024-06-30 类型：复习试卷

进入出卷网下载

一、选择题（每题3分，共30分）

1. 下列多项式相乘，不能用平方差公式计算的是（）

A、（2x﹣3y）（3y﹣2x） B、（﹣2x+3y）（﹣2x﹣3y） C、（x﹣2y）（2y+x） D、（x+3y）（x﹣3y）

查看试题解析
2. 下列整式的运算可以运用平方差公式计算的有（）
① $(2 m + n) (n - 2 m)$ ；② $(a^{2} - 4 b) (4 b - a^{2})$ ；③ $(x + y) (- x - y)$ ； ④ $(3 a + b) (- 3 a + b)$

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 计算(0.1 $x$ +0.3y)(0.1 $x$ -0.3y)的结果为（）

A、 $0.01 x^{2} - 0.09 y^{2}$ B、 $0.01 x^{2} - 0.9 y^{2}$ C、 $0.1 x^{2} - 0.9 y^{2}$ D、 $0.1 x^{2} - 0.3 y^{2}$

查看试题解析
4. 为了应用平方差公式计算(x+2y-1)(x-2y+1)，下列变形正确的是（）

A、[(x+2y)-1)][(x-2y)+1] B、[(x-1)+2yJ[(x+1)-2y] C、[x+(2y-1)][x-(2y-1)] D、[x+(2y-1)][x-(2y+1)]

查看试题解析
5. 计算 $(x - y) (x + y) (x^{2} + y^{2}) (x^{4} + y^{4})$ 的结果是（）

A、 $x^{16} - y^{16}$ B、 $x^{8} - y^{8}$ C、 $x^{7} - y^{7}$ D、 $x^{6} - y^{6}$

查看试题解析
6. 如图，阴影部分是边长为 $a$ 的大正方形中剪去一个边长为 $b$ 的小正方形后所得到的图形，将阴影部分通过割、拼，给出下列 3 种割拼方法，其中能够验证平方差公式的是（）

A、①②
B、②③
C、①③
D、①②③

查看试题解析
7. 若 $M = (x^{2} + 2 x) (x^{2} - 2 x) ， N = (x^{2} + x + 1) (x^{2} - x + 1)$ ，则M与N的大小关系是（）

A、M>N B、M<N C、M=N D、无法确定

查看试题解析
8. 现有一列式子： (1) $55^{2} - 45^{2}$ ； (2) $555^{2} - 445^{2}$ ； (3) $5555^{2} - 4445^{2}$ ；．则第(8)个式子的计算结果用科学记数法可表示为（）

A、1. $1111111 \times 10^{16}$
B、 $1.1111111 \times 10^{27}$
C、 $1.111111 \times 10^{56}$
D、1. $1111111 \times 10^{17}$

查看试题解析
9. 代数式 $2 (3 + 1) (3^{2} + 1) (3^{4} + 1) (3^{8} + 1) (3^{16} + 1) (3^{32} + 1)$ 的末尾数字是（）

A、0 B、1 C、6 D、8

查看试题解析
10. 如图有两张正方形纸片A和B ，图1将B放置在A内部，测得阴影部分面积为2，图2将正方形AB并列放置后构造新正方形，测得阴影部分面积为20，若将3个正方形A和2个正方形B并列放置后构造新正方形如图3，（图2，图3中正方形AB纸片均无重叠部分）则图3阴影部分面积（）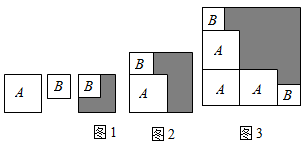

A、22 B、24 C、42 D、44

查看试题解析

二、填空题（每题4分，共24分）

11. 已知 $m - n = 1$ ，则 $m^{2} - n^{2} - 2 n =$

查看试题解析
12. 已知a²-4b²=12，且a-2b=-3，则a+b= ．

查看试题解析
13. 已知 $\{\begin{array}{l} x = a ， \\ y = b \end{array}$ 是方程组 $\{\begin{array}{l} 2 x - 3 y = - 2 ， \\ 2 x + 3 y = 7 \end{array}$ 的解，则代数式 $4 a^{2} - 9 b^{2} =$

查看试题解析
14. 计算： $2023^{2} - 2022^{2} =$

查看试题解析
15. 如图，大正方形 $A B C D$ 和小正方形 $A E F G$ 的周长和为 20 ，且阴影部分的面积是 10 ，则 $B E =$

查看试题解析
16. 两个相同的小长方形按如图1所示的方式摆放，重叠部分是边长为b的正方形，阴影部分的面积为S.四个相同的小长方形按如图2所示的方式摆放，左上角形成的是边长为b的正方形阴影，此阴影部分的面积为 S₁，另一阴影部分的面积为S₂，则S，S₁，S₂之间的数量关系为

查看试题解析

三、计算题（共4题，共23分）

17. 选择适当的公式计算：

(1)、 (-1+4x)(4x-1)

(2)、 (m-3)(-m+3)

(3)、 (-3a+b)(-3a-b)

(4)、 (3a-2b)(-3a-2b)

查看试题解析
18. 计算：

(1)、 $(2 m^{3}) \cdot (3 m^{2} p) \div (2 m p)$ ．

(2)、 ${(a + 1)}^{2} + (a + 3) (a - 3)$ ．

查看试题解析
19. 用简便方法计算

(1)、 $201 1^{2} - 201 0^{2}$ ；

(2)、 $1 7^{2} + 2 \times 17 \times 13 + 1 3^{2}$ ．

查看试题解析
20. 先化简，再求值： ${(1 - 2 x)}^{2} - (x + 1) (1 - x)$ ，其中 $x = - 2$ ．

查看试题解析

四、解答题（共4题，共43分）

21. 试说明：所有周长相同的长方形中，正方形的面积最大[提示：设长方形的周长为 4a，长为（a+x）].

查看试题解析
22. 两个边长分别为a和b的正方形如图放置（图1），其阴影部分面积为 $S_{1}$ ；两个边长分别为a和b的正方形如图放置（图2），其阴影部分面积为 $S_{2}$ ．

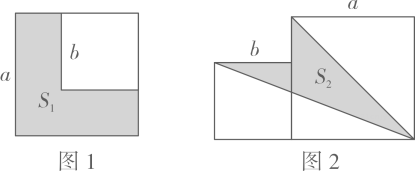(1)、用含a，b的代数式表示 $S_{1}$ ；

(2)、当 $a + b = 8 ， a - b = 2$ 时，求 $S_{1}$ 的值；

(3)、当 $a + b = 8 ， a b = 14$ 时，求出图2中的阴影部分的面积 $S_{2}$ ．

查看试题解析
23. 如图1，边长为 a的大正方形中有一个边长为b的小正方形，把图1中的阴影部分剪拼成一个长方形（如图 2）.

(1)、如图1，可以求出阴影部分的面积为.

(2)、如图2，重新拼成的长方形的宽为，长为，面积为.

(3)、比较左、右两图的阴影部分面积，可以得到公式：

(4)、请应用这个公式完成下列各题：
①已知 $4 m^{2} - n^{2} = 12，2 m + n = 4 ，$ 则 2m-n=
②计算： $2024^{2} - 2022 \times 2026 .$
③计算： $(1 - \frac{1}{2^{2}}) (1 - \frac{1}{3^{2}}) (1 - \frac{1}{4^{2}}) \dots$ $(1 - \frac{1}{2023^{2}}) (1 - \frac{1}{2024^{2}}) .$

查看试题解析
24. 公式的探究与应用：

(1)、如图1所示，可以求出阴影部分的面积是多少(写成两数平方差的形式)？

(2)、若将图1的阴影部分裁剪下来，重新拼成一个如图2所示的长方形，求此长方形的面积(写成多项式乘法的形式)．

(3)、比较两图阴影部分的面积，可以得到一个公式：.

(4)、运用公式计算：(1- $\frac{1}{2^{2}}$ )(1- $\frac{1}{3^{2}}$ )(1- $\frac{1}{4^{2}}$ )……(1- $\frac{1}{9 9^{2}}$ )(1- $\frac{1}{10 0^{2}}$ )

查看试题解析