【培优版】北师大版数学九上1.3正方形的性质与判定 同步练习
试卷更新日期:2024-06-29 类型:同步测试
一、选择题
-
1. 如图,在正方形ABCD外取一点E , 连接AE , BE , DE . 过点A作AE的垂线交DE于点P , . 下列结论:①;②;③点B到直线AE的距离是;④ . 其中所有正确的结论是( )
 A、② ③ B、① ④ C、① ② ④ D、① ② ③ ④2. 如图,在正方形中,点E是上一点,过点E作交于点F , 连接 , , 若 , 则的度数是( )
A、② ③ B、① ④ C、① ② ④ D、① ② ③ ④2. 如图,在正方形中,点E是上一点,过点E作交于点F , 连接 , , 若 , 则的度数是( ) A、 B、 C、 D、3. 如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( )
A、 B、 C、 D、3. 如图,正方形ABCD的边长是4,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值( ) A、 B、2 C、4 D、4. 如图,在正方形中, , 点E在边上,且 , 将沿所在直线翻折得到 , 延长交边于点G , 连接 , , 则下列结论:①;②;③;④;⑤ . 其中正确结论的个数是( )
A、 B、2 C、4 D、4. 如图,在正方形中, , 点E在边上,且 , 将沿所在直线翻折得到 , 延长交边于点G , 连接 , , 则下列结论:①;②;③;④;⑤ . 其中正确结论的个数是( ) A、2 B、3 C、4 D、55. 如图,正方形ABCD中,P是对角线BD上一点,过P作PE⊥BC,PF⊥DC,垂足分别为E、F,连接EF,若EF= , , 点D到AP的距离( )
A、2 B、3 C、4 D、55. 如图,正方形ABCD中,P是对角线BD上一点,过P作PE⊥BC,PF⊥DC,垂足分别为E、F,连接EF,若EF= , , 点D到AP的距离( )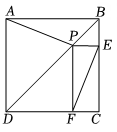 A、 B、 C、 D、6. 如图,四边形是正方形,以为边作等边 , 与相交于点 , 则下列结论中: ; ; 的度数是;≌≌ .
A、 B、 C、 D、6. 如图,四边形是正方形,以为边作等边 , 与相交于点 , 则下列结论中: ; ; 的度数是;≌≌ .正确的有( )个.
 A、 B、 C、 D、7. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( )
A、 B、 C、 D、7. 如图,在正方形中, , 点E,F分别在边上, , 若将四边形沿折叠,点恰好落在边上,则的长度为( ) A、1 B、 C、 D、28. 如图,是正方形的对角线上任意一点,于点 , 于点 , 连接有下列结论:
A、1 B、 C、 D、28. 如图,是正方形的对角线上任意一点,于点 , 于点 , 连接有下列结论:
;
;
一定是等腰三角形;
;
.
其中,正确结论的序号是( ) A、
A、
B、
C、
D、二、填空题
-
9. 如图,正方形中, , O是边的中点,点E是正方形内一动点, , 连接 , 将线段绕点D逆时针旋转得 , 连接 , 则线段长的最小值为 .
 10. 如图, , 四边形是正方形,若 , , 则的面积等于 .
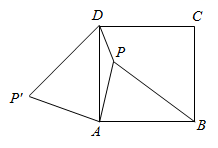
10. 如图, , 四边形是正方形,若 , , 则的面积等于 . 11. 如图,P是正方形 内一点, ,将线段 以点A为旋转中心逆时针旋转 得到线段 ,连接 下列结论:
11. 如图,P是正方形 内一点, ,将线段 以点A为旋转中心逆时针旋转 得到线段 ,连接 下列结论:① 可以由 绕点A逆时针旋转 得到;②点P与 的距离为2;③ ;④ ;⑤ .其中正确的结论是(填序号).
 12. 如图,在正方形ABCD中,点E、F分别在边BC、CD上,且 ,AE交BD于M点,AF交BD于N点.下列结论:① ;② ;③EA平分 ;④ 的周长等于 ,其中正确结论的序号是 .(把你认为所有正确的都填上)
12. 如图,在正方形ABCD中,点E、F分别在边BC、CD上,且 ,AE交BD于M点,AF交BD于N点.下列结论:① ;② ;③EA平分 ;④ 的周长等于 ,其中正确结论的序号是 .(把你认为所有正确的都填上) 13. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ .其中正确结论的序号是
13. 如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点E、F分别在BC和CD上.下列结论:①CE=CF;②∠AEB=75°;③BE+DF=EF;④S正方形ABCD=2+ .其中正确结论的序号是
三、解答题
-
14. 矩形AOBC在平面直角坐标系中的位置如图所示,点A在x轴的负半轴上,点B在y轴的正半轴上,连接AB , 将△ABC沿AB折叠得△ABE , AE交y轴于点D , 线段OD、OA的长是方程x2-7x+12=0的两个根,且OA>OD.
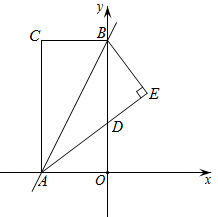 (1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.15. 如图1,在正方形ABCD内作 , AE交BC于点E,AF交CD于点F,连接EF,过点A作 , 垂足为H.
(1)、请直接写出点A的坐标为 , 点D的坐标为;(2)、点P为直线AB上一点,连接PO、PD , 当△POD的周长最小时,求点P的坐标;(3)、点M在x轴上,点N在直线AB上,坐标平面内是否在点Q , 使以B、M、N、Q为顶点的四边形为正方形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.15. 如图1,在正方形ABCD内作 , AE交BC于点E,AF交CD于点F,连接EF,过点A作 , 垂足为H.图1
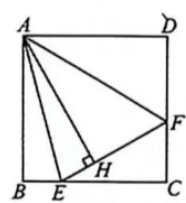 图2
图2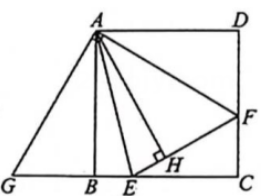 图3
图3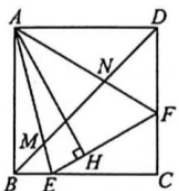 (1)、如图2,将绕点A顺时针旋转得到.
(1)、如图2,将绕点A顺时针旋转得到.①求证:.
②若 , , 求AH的长.
(2)、如图3,连接BD交AE于点M,交AF与点N,请探究并猜想:线段BM,MN,ND之间有什么关系?请说明理由?16. 如图1,在平面直角坐标系中,直线AB交两坐标轴于A、B两点(OA>OB),且OA、OB的长是一元二次方程x2﹣7x+12=0的两根.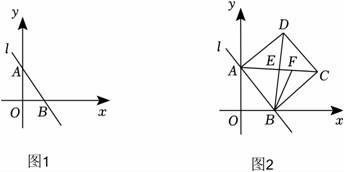 (1)、求直线AB的解析式;(2)、以线段AB为边作正方形ABCD(如图2),对角线AC、BD交于点E,∠CBD的平分线BF交AC于F,求CF的长;(3)、若M是y轴上任一点,点N是坐标平面内一点,若以A、B、M、N为顶点的四边形是菱形,请直接写出N点的坐标.17. 如图①在正方形中,点是对角线上一点.点在的延长线上,且交于点.
(1)、求直线AB的解析式;(2)、以线段AB为边作正方形ABCD(如图2),对角线AC、BD交于点E,∠CBD的平分线BF交AC于F,求CF的长;(3)、若M是y轴上任一点,点N是坐标平面内一点,若以A、B、M、N为顶点的四边形是菱形,请直接写出N点的坐标.17. 如图①在正方形中,点是对角线上一点.点在的延长线上,且交于点. (1)、求证:;(2)、求的度数;(3)、如图②,把正方形改为菱形,其他条件不变,当 , 连接.试探究线段与线段的数量关系,并说明理由.18. 阅读以下材料,并按要求完成相应的任务:
(1)、求证:;(2)、求的度数;(3)、如图②,把正方形改为菱形,其他条件不变,当 , 连接.试探究线段与线段的数量关系,并说明理由.18. 阅读以下材料,并按要求完成相应的任务:从正方形的一个顶点引出夹角为的两条射线,并连接它们与该顶点的两对边的交点构成的基本平面几何模型称为半角模型.半角模型可证出多个几何结论,例如:
如图1,在正方形中,以为顶点的 , 、与、边分别交于、两点.易证得: .
大致证明思路:如图2,将绕点顺时针旋转 , 得到 , 由可得、、三点共线, , 进而可证明 , 故 .
任务:

如图3,在四边形中, , , , 以为顶点的 , 、与、边分别交于、两点.请参照阅读材料中的解题方法,你认为结论是否依然成立,若成立,请写出证明过程;若不成立,请说明理由.