【培优版】北师大版数学九上1.2矩形的性质与判定同步练习

试卷更新日期：2024-06-29 类型：同步测试

进入出卷网下载

一、选择题

1. 如图，在矩形 $A B C D$ 中， $E$ 、 $F$ 分别是边 $A B$ 、 $C D$ 上的点， $A E = C F$ ， $E F$ 与对角线 $A C$ 交于点 $O$ ，且 $B E = B F$ ， $∠ B E F = 2 ∠ B A C$ ， $F C = \sqrt{3}$ ，则 $A B$ 的长为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{3}$ C、 $4 \sqrt{3}$ D、6

查看试题解析
2. 如图，矩形 $A B C D$ 中， $A B = 5$ ， $A D = 6$ ，点P为平面内一点，且 $B P = 2$ ，点Q为CD上一个动点，则 $A Q + P Q$ 的最小值为（）

A、11 B、 $5 \sqrt{2} - 2$ C、 $\sqrt{103} - 2$ D、13

查看试题解析
3. 如图，在 ▱ ABCD中，有下列条件：①AC=BD.②∠1+∠3=90°.③OB= $\frac{1}{2}$ AC.④∠1=∠2.其中能判定 ▱ ABCD是矩形的有（）

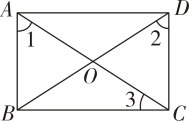A、① B、①②③ C、②③④ D、①②③④

查看试题解析
4. 矩形纸片ABCD中，AB=5，AD=4，将纸片折叠，使点B落在边CD上的B′处，折痕为AE．延长B′E交AB的延长线于M，折痕AE上有点P，下列五个结论中正确的有（）个.
①∠M=∠DAB′；②PB=PB′；③ $A E = \frac{5 \sqrt{5}}{2}$ ；④MB′=CD；⑤若B′P⊥CD，则EB′=B′P．

A、2 B、3 C、4 D、5

查看试题解析
5. 如图，在矩形ABCD中，AC，BD相交于点O，AE平分∠BAD交BC于点E，若∠CAE＝15°，OA＝6，则BE的长为（　　）

A、5 B、6 C、7 D、8

查看试题解析
6. 如图，将矩形纸片 $A B C D$ 沿对角线 $A C$ 对折，使得点B落在点E处， $C E$ 交 $A D$ 于点F，若 $C E$ 平分 $∠ A C D$ ， $A F = 2$ ，则 $C D$ 的长是（）

A、1.5 B、 $\sqrt{3}$ C、 $\frac{\sqrt{3}}{2} + 1$ D、 $\frac{\sqrt{3} + 1}{2}$

查看试题解析
7. 如图，在矩形ABCD中， $A B = 2$ ， $B C = 4$ ， $F$ 为 $B C$ 中点， $P$ 是线段 $B F$ 上一点，设 $B P = m (0 < m \leq 2)$ ，连接 $A P$ 并将它绕点 $P$ 顺时针旋转90°得到线段 $P E$ ，连接 $C E$ ， $E F$ ，则在点 $P$ 从点 $B$ 向点 $F$ 运动的过程中，下列说法错误的是（）

A、 $∠ E F C = 45 °$ B、点 $D$ 始终在直线 $E F$ 上 C、 $△ F C E$ 的面积为m D、 $C E$ 的最小值为 $\sqrt{3}$

查看试题解析
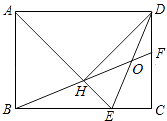
8. 如图，在矩形ABCD中，AD= $\sqrt{2}$ AB，∠BAD的平分线交BC于点E，DH⊥AE于点H，连接BH并延长交CD于点F，连接DE交BF于点O，下列结论：
①∠AED=∠CED；②OE=OD；③BH=HF；④BC﹣CF=2HE；⑤AB=HF，
其中正确的有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

9. 如图，在 $△ A B C$ 中， $∠ C = 90 ° ， A C = B C = 6$ ． P为边 $A B$ 上一动点，作 $P D ⊥ B C$ 于点D， $P E ⊥ A C$ 于点E，则 $D E$ 的最小值为．

查看试题解析
10. 如图，在矩形ABCD 中，E是AD的中点，连结BE，将△ABE 沿BE 翻折得到△FBE，EF 交 BC 于点H，延长BF，DC 相交于点G.若DG=8，BC=12，则FH=.

查看试题解析
11. 如图 $1$ 是七巧板图案，现将它剪拼成一个“台灯”造型 $($ 如图 $2)$ ，过该造型的上下左侧五点作矩形 $A B C D$ ，使得 $\frac{A B}{B C} = \frac{3}{5}$ ，点 $N$ 为 $P Q$ 的中点，并且在矩形内右上角部分留出正方形 $E F G H$ 作为印章区域 $(E H / / A D ， H G / / C D)$ ，形成一幅装饰画，则矩形 $A B C D$ 的周长为 $c m .$ 若点 $M$ ， $N$ ， $E$ 在同一直线上，且点 $H$ 到 $A D$ 的距离与到 $C D$ 的距离相等，则印章区域的边长为 $c m$ ．

查看试题解析
12. 如图，在矩形ABCD中， $A B = 2$ ， $A D = 3$ ，动点P在矩形的边上沿 $B \to C \to D \to A$ 运动。当点P不与点A、B重合时，将 $△ A B P$ 沿AP对折，得到 $△ A B^{'} P$ ，连接 $C B^{'}$ ，则在点P的运动过程中，线段 $C B^{'}$ 的最小值为.

查看试题解析
13. 如图1，有一张矩形纸片 $A B C D$ ，已知 $A B = 10$ ， $A D = 12$ ，现将纸片进行如下操作：现将纸片沿折痕 $B F$ 进行折叠，使点 $A$ 落在 $B C$ 边上的点 $E$ 处，点 $F$ 在 $A D$ 上（如图2），则 $D F =$ ；然后将 $△ F B E$ 绕点 $F$ 旋转到 $△ F M N$ ，当 $M N$ 过点 $C$ 时旋转停止，则 $E N$ 的长度为．

查看试题解析

三、解答题

14. 如图，在平行四边形ABCD中，AB=5，BC=7，∠ACB=45°，AC＞AB ， E ， F为对角线AC上的两点(点E与A、C、F都不重合)，AE=CF ， EM⊥BC于点M ， FN⊥AD于点N ，连结EN ， FM ．

(1)、求证：四边形EMFN是平行四边形．

(2)、四边形EMFN能否成为矩形？四边形EMFN能否成为菱形？请直接写出答案．

(3)、连结MN ，作点C关于MN的对称点C^' ，若点C^'落在边AB上，求AE的长.

查看试题解析
15. 如图1，将矩形纸片 $A B C D$ 对折， $A B$ 与 $C D$ 重合，展开后，折痕为 $E F$ ．再次折叠，折痕 $C N$ 经过点 $C$ ，且 $C N$ 交 $E F$ 于点 $O$ ，使点 $B$ 落在 $E F$ 上的点 $G$ 处，连接 $B G$ 、 $C G$ ，点 $F$ 落在 $C G$ 上的点 $H$ 处，连接 $B H$ ．

(1)、求 $∠ A B G$ 的度数；

(2)、求证： $B H ⊥ C G$ ；

(3)、如图2，在矩形纸片 $A B C D$ 中， $K$ 是边 $C D$ 上的一点，连接 $B K$ ，在 $B C$ 上取一点 $P$ ，折叠纸片，使 $B$ 、 $P$ 两点重合，展开后，折痕为 $E F$ ．沿着直线 $M N$ 折叠纸片，使点 $B$ 落在 $E F$ 上的点 $G$ 处，点 $P$ 落在 $B K$ 上的点 $Q$ 处，连接 $B G$ 、 $G Q$ ， $M N$ 交 $E F$ 于点 $O$ ．试探究 $∠ B Q G$ 与 $∠ A B G$ 之间的数量关系．

查看试题解析
16. 如图，在 $△ A B C$ 中，O是边 $A C$ 上的一个动点，过点O作直线 $M N ∥ B C$ ，交 $∠ A C B$ 的平分线于点E ，交 $△ A B C$ 的外角 $∠ A C D$ 的平分线于点F ．

(1)、求证： $O E = O F$ ；

(2)、若 $C E = 12, C F = 5$ ，求 $O C$ 的长；

(3)、连接 $A E, A F$ ，当点O在边 $A C$ 上运动到什么位置时，四边形 $A E C F$ 是矩形？请说明理由．

查看试题解析
17. 在平面直角坐标系中，四边形 $A O B C$ 是矩形，点 $O (0 ， 0)$ ，点 $A (6 ， 0)$ ，点 $B (0 ， 8)$ ．以点A为中心，顺时针旋转矩形 $A O B C$ ，得到矩形 $A D E F$ ，点 $O ， B ， C$ 的对应点分别为 $D ， E ， F$ ，记旋转角为 $α (0 ° < α < 90 °)$ ．

(1)、如图1，当 $α = 30 °$ 时，求点D的坐标；

(2)、如图2，当点E落在 $A C$ 的延长线上时，求点D的坐标；

(3)、如图3，当点D落在线段 $O C$ 上时，求点E的坐标．

查看试题解析
18. 已知矩形 $A B C D$ ， $A B = 3$ ， $B C = 5$ ，将矩形 $A B C D$ 绕A顺时针旋转 $α (0 ° < α < 180 °)$ ，得到矩形 $A E F G$ ，点B的对应点是点E ，点C的对应点是点F ，点D的对应点是点G ．

(1)、如图①；当 $α = 90 °$ 时，连接 $C F$ ，求 $C F$ 的长；

(2)、如图②，当边 $E F'$ 经过点D时，延长 $F E$ 交 $B C$ 于点P ，求 $E P$ 的长；

(3)、连接 $C F$ ，点M是 $C F$ 的中点，连接 $B M$ ，在旋转过程中，线段 $B M$ 的最大值．

查看试题解析

【培优版】北师大版数学九上1.2矩形的性质与判定 同步练习

一、选择题

二、填空题

三、解答题

【培优版】北师大版数学九上1.2矩形的性质与判定同步练习