【提升版】北师大版数学九上 1.2矩形的性质与判定 同步练习
试卷更新日期：2024-06-29 类型：同步测试
一、选择题
-
1. 如图，点E，F，G，H分别为四边形ABCD的边AB，BC，CD，DA的中点．下列三种说法：
① .四边形EFGH一定是平行四边形；
②.若AC＝BD，则四边形EFGH 是菱形；
③.若AC⊥BD，则四边形EFGH是矩形．
其中正确的是（ ）
A、① B、①② C、①③ D、①②③2. 如图，已知四边形ABCD是平行四边形，下列结论中不正确的是（ ）
A、当时，它是菱形 B、当时，它是菱形 C、当时，它是正方形 D、当时，它是矩形3. 依据所标数据，下列四边形不一定为矩形的是（ ）A、
B、
C、
D、
4. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为（ ）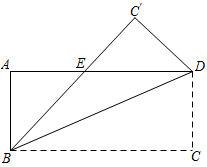
A、3 B、4 C、5 D、65. 如图，已知的四个内角的平分线分别交于点、、、 ， 则四边形的形状是（ ）
A、平行四边形 B、矩形 C、菱形 D、正方形6. 如图，在Rt△ABC中，∠ACB=90° ， 点E ， 点F分别是AC ， BC的中点，D是斜边AB上一点，添加下列条件可以使四边形DECF成为矩形的是 ( )
A、AD=BD B、∠ACD=∠BCD C、CD⊥AB D、CD=AC7. 如图，在△ABC中，AB=3，AC=4，BC=5，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，M为EF中点，则AM的最小值为（ ）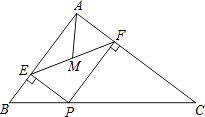
A、 B、 C、 D、8. 如图，矩形ABCD中，对角线AC，BD相交于点O，AD＝2 ， ∠COB＝60°，BF⊥AC，交AC于点M，交CD于点F，延长FO交AB于点E，则下列结论：①FO＝FC；②四边形EBFD是菱形；③△OBE≌△CBF；④MB＝3．其中结论正确的序号是（ ）
A、②③④ B、①②③ C、①④ D、①②③④二、填空题
-
9. 将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝6，则BC的长为 ．
10.如图，矩形ABCD中，AB=6，BC=8，E是BC边上的一定点，P是CD边上的一动点（不与点C、D重合），M，N分别是AE、PE的中点，记MN的长度为a，在点P运动过程中，a不断变化，则a的取值范围是 ．
11. 如图，在矩形中， ， ， 对角线相交于点E ， 将沿着翻折到 ， 连接 ， 则的长为 ．
12. 如图，小刘同学在折叠矩形ABCD中发现，当E是AD边的中点时候，将△ABE沿BE折叠后得到△GBE ， 延长BG ， 交CD于点F ． 若连接EF ， 则△EGF≌△EDF ， CF＝7，DF＝9，请你帮她算BC的长 ．
13. 如图，在矩形中， ， ， 将其折叠，使边落在对角线上，得到折痕 ， 则点到点的距离为 ．
三、解答题
-
14. 如图，过菱形的顶点A作于点E ， 延长至点F ， 使 ， 连接 ．
(1)、求证：四边形是矩形；(2)、若 ， 求的长．15. 如图，矩形的对角线交于点F ， 延长到点C ， 使 ， 延长到点D ， 使 ， 连接
(1)、求证：四边形是菱形；(2)、若 ， 求菱形的面积．16. 如图，已知矩形ABCD，AD=4，CD=10，P是AB上一动点，M、N、E分别是PD、PC、CD的中点．
(1)、求证：四边形PMEN是平行四边形；(2)、请直接写出当AP为何值时，四边形PMEN是菱形；(3)、四边形PMEN有可能是矩形吗？若有可能，求出AP的长；若不可能，请说明理由．17. 如图，将矩形ABCD绕点B旋转得到矩形BEFG，点E在AD上，延长DA交GF于点H．
(1)、求证：△ABE≌△FEH；(2)、连接BH，若∠EBC＝30°，求∠ABH的度数．四、实践探究题
-
18. 综合与实践
问题情境：在综合与实践课上，老师让同学们以“矩形纸片的折叠”为主题开展数学活动，请你解答各小组活动中产生的问题如图所示，在矩形中， ， ， 将矩形纸片进行折叠：
(1)、问题解决：如图 ， 奋斗小组将该矩形沿对角线折叠，点的对应点为点 ， 则 ， ；(2)、实践探究：如图 ， 希望小组将矩形沿着点 ， 分别在边 ， 边上所在的直线折叠，点的对应点为点 ， 连接 ，试判断四边形的形状，并说明理由；
求折痕的长．